本文最后更新于：2020年6月25日 晚上

Harris特征点检测器-兴趣点检测

特则点又称为兴趣点或角点，通常具有旋转不变性和光照不变性和视角不变性等优点，是图像的重要特征之一，常被应用到目标匹配、目标跟踪、三维重建等应用中。

点特征主要是指图像中的明显点，如突出的角点、边缘端点、权值点等等。

兴趣点提取(检测)算子是用于点特征提取的算子，常用的有

  • Harris角点检测：用于检测角点
  • FAST特征检测：用于检测角点
  • SIFT特征检测：用于检测斑点
  • SURF特征检测：用于检测角点
  • BRIEF特征检测：用于检测斑点
  • ORB：该算法代表带方向的FAST算法和具有旋转不变性的BRIEF算法

特征匹配：

  • 暴力(Brute-Force)匹配法
  • 基于FLANN匹配法

一、Harris特征点检测算法的思想和数学原理

1.1 基础知识

  • 角点

    左图表示一个平坦区域，在各个方向移动，窗口内像素值均没有太大变化；

    中图表示一个边缘特征(Edges)，若沿着水平方向移动(梯度方向)，像素值会发生跳变；若沿着边缘移动(平行于边缘)，像素值不变发生变化；

    右图表示一个角(Corners)，它朝哪个方向移动，像素值都会发生很大变化。即为角点。

在这里插入图片描述

  • 图像梯度:图像局部内，图像梯度越大表示该局部内像素值变化越大。图形梯度在数学上可用微分或者积分表示,使用差分来近似导数：$G_x(x,y)=H(x+1,y)-H(x-1,y)$,
  • 补充：对图像求梯度通常是考虑图像的每个像素的某个领域内的灰度变化，因此通常对原始图像中像素某个领域设置梯度算子，然后采用小区域模板进行卷积计算，常用的有Prewitt算子、Sobel算子、Robinson算子、Laplace算子等。

1.2 Harris角点检测算法原理

1.2.1 计算窗口内部的像素值变化量$E(x,y)$

建立数学模型，确定哪些窗口会引起较大的灰度值变化

窗口$W$对应的像素坐标位置$(x,y)$，窗口的大小决定了有多少位置。

像素位置坐标$(x,y)$对应的像素灰度值为$I(x,y)$，窗口分别向$x$和$y$方向上移动$(u,v)$，到达$(x+u,y+v)$上，对应的像素灰度值$I(x+u,y+v)$。

窗口移动引起的灰度值的变化量为$I(x+u,y+v)-I(x,y)$。

$(x,y)$位置的窗口函数为$w(x,y)$。即为窗口内各像素的权重。

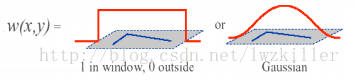
image-20200623143300133

窗口移动(u,v)引起的灰度值的加权变化量：

根据二维泰勒公式展开：

其中$I_x,I_y$分别为窗口内像素点$(x,y)$在$x$方向上和$y$方向上的梯度值。矩阵$M$为：

最后使用实对称矩阵对角化处理后得到我们想要的结果。

1.2.2 计算对应的角点响应函数$R$

通过矩阵的梯度变化可以得到协方差矩阵M，协方差矩阵M决定了灰度值的加权变化量。因此通过计算角点响应函数R得到每个窗口对应的得分:

其中$det(M)=\lambda_1\lambda_2$为矩阵的行列式，$trace(M)=\lambda_1+\lambda_2$为矩阵的迹。

$k$是一个经验常数，需要经验确定它的合适大小，通常在(0.04,0.06)之间取值。

1.2.3 角点判定

根据R值判断窗口是平面、边缘还是角点：

  • 平面：$|R|$值非常小，$\lambda_1$和$\lambda_2$都较小，窗口区域的像素点的梯度变化小。
  • 边缘：$|R|$值为负数，$\lambda_1 \gg \lambda_2$或$\lambda_2 \gg \lambda_1$，像素点的某个方向的梯度幅值变化比较明显，另一个方向上的梯度变化比较弱。
  • 角点：$|R|$值很大，$(I_x,I_y)$对应的$\lambda_1$和$\lambda_2$都很大。像素点的梯度分布比较散，梯度变化程度比较大。

如下图所示：

在这里插入图片描述

Harris角点检测：设定一个阈值，高于阈值的像素对应角点。

  • 补充：角点的非极大值原理—在一个窗口内，如果有很多角点则用值最大的那个角点，其他的角点都删除。

1.3 Shi-Tomasi角点检测器

Shi-Tomasi 角点检测：《Good_Features_to_Track》论文提出的Harris改进版。

Harris角点检测中每个窗口的分数公式：$R=\lambda_1\lambda_2 - k(\lambda_1+\lambda_2)^2$

缺陷：Harris角点检测算法的稳定性和k值有关，但k是经验值，不好设定最佳值。

改进：角点稳定性与矩阵$M$的较小特征值有关，Shi-Tomasi 直接采用较小的特征值作为分数。(如此一来就不用调整k值啦)

Shi-Tomasi角点检测中每个窗口的分数公式：$R=min(\lambda_1,\lambda_2)$

判定角点的方式不变：分数大于设定的阈值，即为角点。

二、OpenCV的Harris算子进行兴趣点检测

2.1 Harris角点检测

opencv提供了实现Harris角点检测函数：cv2.cornerHarris，下面调用该接口进行Harris特征点检测。

函数：cv2.cornerHarris(src, blockSize, ksize, k[, dst[, borderType]])​

函数功能：对于每一个像素 $(x,y)$，在 ($blockSize$ x $blockSize$) 邻域内，计算梯度图的协方差矩阵$M(x,y)$，通过计算角点响应函数得到结果图。该结果图的局部最大值即图像中的角点。

函数参数：

  • src:待检测的灰度图像(float32类型)
  • blockSize:用于角点检测的领域大小，即窗口尺寸
  • ksize:用于计算梯度图的Sobel算子的尺寸
  • k:用于计算角点响应函数的参数k，取值范围在0.04~0.06之间

待检测的图片：

image1

import cv2 as cv
from matplotlib import pyplot as plt
import numpy as np

# 检测参数
block_size = 3
sobel_size = 3
k = 0.06

image = cv.imread('image1.jpg')
print(image.shape)
height = image.shape[0]
width = image.shape[1]
channels = image.shape[2]
print("width: %s height: %s channel: %s"%(width, height, channels))
# 将图像转换为灰度图
gray_img = cv.cvtColor(image, cv.COLOR_BGR2GRAY)
# 将数据格式转换为32位浮点数
gray_img = np.float32(gray_img)

# 使用合适值作为输入参数检测角点，得到的结果图用来标出角点
corners_img = cv.cornerHarris(gray_img, block_size, sobel_size, k)

输出：

(225, 225, 3)
width: 225 height: 225 channel: 3
kernel = cv.getStructuringElement(cv.MORPH_RECT,(3,3))
dst = cv.dilate(corners_img, kernel)
# dst = cv.dilate(corners_img,None)
# image[dst>0.05*dst.max()] = [255,0,0]
# num = dst > 0.05 * dst.max()
# count = np.sum(num)
# print(count)
count = 0
for r in range(height):
    for c in range(width):
        pix = dst[r,c]
        # 阈值，蓝色标记角点
        if pix > 0.05 * dst.max():
            cv.circle(image,(c,r),2,(255,0,0),-1)
            count += 1
print(count)
cv.imwrite('harris_img1.jpg',image)

输出：

741

处理后图片如下：

harris_img1

# 使用点画图，点小一点，好看一丢丢把。。。
image[dst>0.05*dst.max()] = [255,0,0]

harris_img1

2.2 Shi-Tomasi角点检测

opencv提供了实现Shi-Tomasi 角点检测函数：cv2.goodFeaturesToTrack()，下面调用该接口进行Harris特征点检测。

函数：goodFeaturesToTrack(image, maxCorners, qualityLevel, minDistance[, corners[, mask[, blockSize[, useHarrisDetector[, k]]]]])

函数功能：流程大体与Harris相似。不同之处在于窗口分数计算公式不同。在检测到的角点中，所有低于质量水平的角点都会被忽略，合格角点按角点质量进行降序排列，保留质量最高的一个角点，将它附近（最小距离之内）的角点都删掉（类似于非极大值抑制），按这样的方式最后得到 N 个最佳角点。

函数参数：

  • image：输入灰度图像，float32类型
  • maxCorners：返回角点的最大数目，值为0表表示不设置最大值限制，返回所有检测到的角点。
  • qualityLevel：质量系数（小于1.0的正数，一般在0.01-0.1之间），表示可接受角点的最低质量水平。该系数乘以最好的角点分数（也就是上面较小的那个特征值），作为可接受的最小分数；例如，如果最好的角点分数值为1500且质量系数为0.01，那么所有质量分数小于15的角都将被忽略。
  • minDistance：角之间最小欧式距离，忽略小于此距离的点。
  • corners：输出角点坐标
  • mask：可选的感兴趣区域，指定想要检测角点的区域。
  • blockSize：默认为3，角点检测的邻域大小（窗口尺寸）
  • useHarrisDetector：用于指定角点检测的方法，如果是true则使用Harris角点检测，false则使用Shi Tomasi算法。默认为False。
  • k：默认为0.04，Harris角点检测时使用。
import numpy as np
import cv2
maxCorners = 600
qualityLevel = 0.01
minDistance = 10

img = cv2.imread('image1.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
corners = cv2.goodFeaturesToTrack(gray, maxCorners, qualityLevel, minDistance)
corners = np.int0(corners)
count = 0
for i in corners:
    x,y = i.ravel()
    cv2.circle(img,(x,y), 2, (255,0,0),-1)
    # img[y,x] = [255,0,0]
    count += 1
cv.imwrite('Shi-Tomasi.jpg',img)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
print(count)

总结

Harris和Shi-Tomasi都是基于梯度计算的角点检测方式。

Harris角点检测的性质：

  • 阈值界定角点数量

  • Harris角点算子对亮度和对比度的变化不敏感

    因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量。

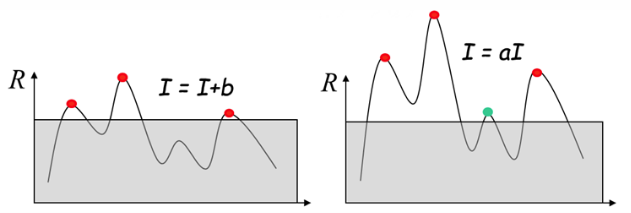
    image-20200623145505861

    左图表示亮度变化，右图表示对比度变化。

  • Harris角点检测算子具有旋转不变性

    Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值RR也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

  • Harris角点检测算子不具有尺度不变性

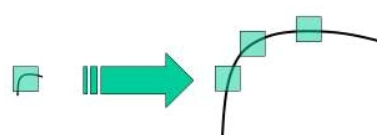
    image-20200623003833148

    如上图所示，当图像被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点。

基于梯度的角点检测器的缺点：计算复杂度高、图像中的噪声阻碍梯度计算。

参考

Task01 Harris特征点检测器-兴趣点检测

角点检测：Harris 与 Shi-Tomasi

Harris角点检测原理(赋源码)