如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如：

[2,3,4]的中位数是3
[2,3]的中位数是(2+3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

• void addNum(int num) - 从数据流中添加一个整数到数据结构中。
• double findMedian() - 返回目前所有元素的中位数。

示例1：

输入：
["MedianFinder","addNum","findMedian","addNum","findMedian"]
[[],[1],[2],[],[3],[]]
输出：[null,null,null,1.50000,null,2.00000]

示例2：

输入：
["MedianFinder","addNum","findMedian","addNum","findMedian"]
[[],[2],[],[3],[]]
输出：[null,null,2.00000,null,2.50000]

限制：

• 最多会对$addNum$，$findMedian$进行50000次调用。

class MedianFinder:
	def __init__(self):
	"""
	initialize your data structure here.
	"""
	def addNum(self, num):
	def findMedian(self):
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()

解题思路：

给定一个长度为$N$的无序数组，其中位数的计算方法：首先对数组执行排序(使用O(NlogN)时间)，然后返回中间元素即可(使用O(1)时间)。

针对本题，根据以上思路，可以将数据流保存在一个列表中，并在添加元素时保持数组有序。此方法的时间复杂度为$O(N)$，其中包括：查找元素插入位置$O(logN)$(二分查找)、向数组某位置插入元素$O(N)$(插入位置之后的元素都需要向后移动一位)。

借助堆可进一步优化时间复杂度。

建立一个小顶堆A和大顶堆B，各保存列表的一半元素，且规定：

• A保存较大的一半，长度为$\frac{N}{2}$（N为偶数）或$\frac{N+1}{2}$(N为奇数)；
• B保存较小的一半，长度为$\frac{N}{2}$(N为偶数)或$\frac{N-1}{2}$)(N为奇数)；

随后，中位数仅根据A,B的堆顶元素计算得到。

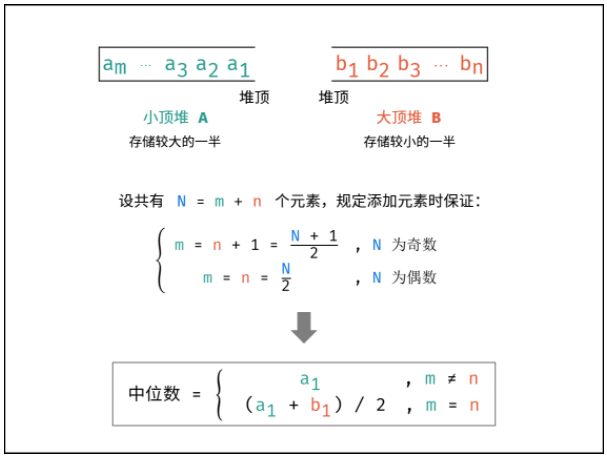
算法流程：

设元素总数为N=m+n，其中m和n分别是A和B中的元素个数。

addNum(num)函数：

1. 当$m=n$(即$N$为偶数)：需向A添加一个元素。实现方法：将新元素$num$插入至B，再将B堆顶元素插入至A;
2. 当$m \neq n$(即N为奇数)：需向B添加一个元素。实现方法：将新元素num插入至A，再将A堆顶元素插入至B;

假设插入数字num遇到情况1.。由于num可能属于”较小的一半”(即属于B)，因此不能将num直接插入至A。而应先将num插入至B，再将B堆顶元素插入至A。这样就可以始终保持A保存较大一半、B保持较小一半。

findMedian()函数：

1. 当$m=n$($N$为偶数)：则中位数为(A的堆顶元素+B的堆顶元素)/2。
2. 当$m \neq n$($N$为奇数)：则中位数为A的堆顶元素。

复杂度分析：

• 时间复杂度：
  • 查找中位数$O(1)$：获取堆顶元素使用$O(1)$时间；
  • 添加元素$O(logN)$：堆的插入和弹出操作使用$O(logN)$时间。
• 空间复杂度$O(N)$：其中$N$为数据流汇总的元素数量，小顶堆A和大顶堆B最多同时保存$N$个元素。

代码：

Python中heapq模块是小顶堆。实现大顶堆方法：小顶堆的插入和弹出操作均将元素取反即可。

from heapq import *
class MedianFinder:
    def __init__(self):
        self.A = [] # 小顶堆，保存较大的一半
        self.B = [] # 大顶堆，保存较小的一半
    def addNum(self, num):
        if len(self.A) != len(self.B):
            heappush(self.A, num)
            heappush(self.B, -heappop(self.A))
        else:
            heappush(self.B, -num)
            heappush(self.A, -heappop(self.B))
   def findMedian(self):
		return self.A[0] if len(A) != len(B) else (self.A[0] - self.B[0]) / 2.0

使用heappushpop优化heappush+heappop

from heapq import *
class MedianFinder:
    def __init__(self):
        self.A = [] # 小顶堆，保存较大的一半
        self.B = [] # 大顶堆，保存较小的一半
    def addNum(self, num):
        if len(self.A) != len(self.B):
            heappush(self.B, -heappushpop(self.A, num))
        else:
            heappush(self.A, -heappushpop(self.B, -num))
   def findMedian(self):
		return self.A[0] if len(A) != len(B) else (self.A[0] - self.B[0]) / 2.0