本文最后更新于:2020年7月8日 下午
169.多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于$\lfloor \dfrac{n}{2} \rfloor$的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [3,2,3]
输出: 3示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2说明
本题题目没有给出数据范围,最简单的暴力方法(枚举数据中的每个元素,再遍历一遍数组统计其出现次数,时间复杂度为$O(N^2)$的算法),会超出时间限制。
我首先想到的就是哈希表。
方法一:哈希表
思路
已知出现次数最多的元素大于$\lfloor \dfrac{n}{2} \rfloor$次,可以用哈希表来快速统计每个元素出现的次数。
算法
使用哈希映射(HashMap)来存储每个元素以及出现的次数。对于哈希映射中的每个键值对,键表示一个元素,值表示该元素出现的次数。
用一个循环遍历数组nums并将数组中的每个元素加入哈希映射中。在这之后,遍历哈希映射中的所有键值对,返回值最大的键。同样也可以在遍历数组nums时候使用打擂台的方法,维护最大的值,这样省去了最后对哈希映射的遍历。
代码
class Solution:
def majorityElement(self, nums):
counts = collections.Counter(nums)
return max(counts.keys(), key=counts.get)复杂度分析
- 时间复杂度:$O(n)$,其中 $n$是数组
nums的长度。我们遍历数组nums一次,对于nums中的每一个元素,将其插入哈希表都只需要常数时间。如果在遍历时没有维护最大值,在遍历结束后还需要对哈希表进行遍历,因为哈希表中占用的空间为$O(n)$(可参考下文的空间复杂度分析),那么遍历的时间不会超过$O(n)$。因此总时间复杂度为$O(n)$。
- 空间复杂度:$O(n)$。哈希表最多包含$n - \lfloor \dfrac{n}{2} \rfloor$个键值对,所以占用的空间为$O(n)$。这是因为任意一个长度为$n$的数组最多只能包含$n$个不同的值,但题中保证
nums一定有一个众数,会占用(最少)$\lfloor \dfrac{n}{2} \rfloor + 1$个数字。因此最多有$n - (\lfloor \dfrac{n}{2} \rfloor + 1)$个不同的其他数字,所以最多有$n - \lfloor \dfrac{n}{2} \rfloor$个不同的元素。
方法二:排序
思路
如果将数组如果将数组nums中的所有元素按照单调递增或单调递减的顺序排序,那么下标为 $\lfloor \dfrac{n}{2} \rfloor$的元素(下标从 0 开始)一定是众数。
算法
先将nums数组排序,返回$\lfloor \dfrac{n}{2} \rfloor$下标对应的元素。下图解释了这种策略有效的原因,第一个例子是$n$为奇数的情况,第二个例子是$n$为偶数的情况。
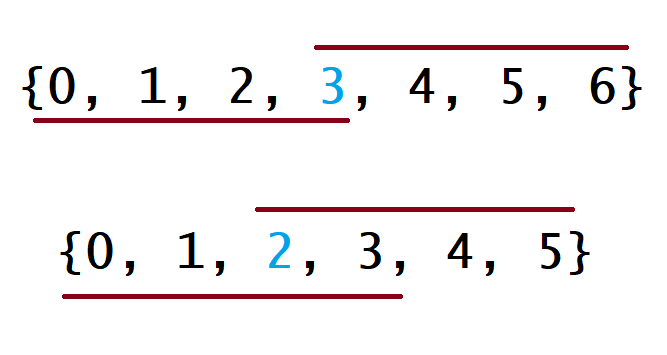
对于每种情况,数组下划线表示众数是数组最小值时覆盖的下标,数组上划线表示众数时数组最大值时覆盖的下标。其他情况,这条线会在这两种极端情况的中间,即下划线右移,上划线左移。两个极端情况会在下标为$\lfloor \dfrac{n}{2} \rfloor$的地方重叠。因此,无论众数时多少,返回$\lfloor \dfrac{n}{2} \rfloor$下标对应的值都是正确的。
代码
class Solution:
def majorityElement(self, nums):
nums.sort()
return nums[len(nums)//2]复杂度分析
- 时间复杂度:$O(nlogn)$。将数组排序的时间复杂度为$O(nlogn)$。
- 空间复杂度:$O(nlogn)$。雨果使用语言自带的排序算法,需要使用$O(nlogn)$的栈空间,如果自己编写堆排序,则只需要$O(1)$的额外空间。
方法三:随机化
思路
因为超过$\lfloor \dfrac{n}{2} \rfloor$的数组下标被众数占据了,这样我们随机挑选一个下标对应的元素并验证,有很大的概率能找到众数。
算法
由于一个给定的下标对应的数字很有可能是众数,随机挑选一个下标,检查它是否是众数,如果是就返回,否则继续随机挑选。
代码
import random
class Solution:
def majorityElement(self, nums):
majority_count = len(nums)//2
while True:
candidate = random.choice(nums)
if sum(1 for elem in nums if elem == candidate) > majority_count:
return candidate时间复杂度:理论上最坏情况下的时间复杂度为$O(\infty)$,因为如果我们的运气很差,这个算法会一直找不到众数,随机挑选无穷多次,所以最坏时间复杂度是没有上限的。然而,运行的期望时间是线性的。
为了更简单地分析,先说服你自己:由于众数占据超过数组一半的位置,期望的随机次数会小于众数占据数组恰好一半的情况。因此,我们可以计算随机的期望次数(下标为prob为原问题,mod为众数恰好占据数组一半数目的问题):
计算方法为:当众数恰好占据数组的一半时,第一次随机我们有$\frac{1}{2}$的概率找到众数,如果没有找到,则第二次随机时,也就是第二次找到众数的概率为$\frac{1}{4}$,以此类推。因此期望的次数为$i \frac{1}{2^i}$的和,可以计算出这个和为2,说明*期望的随机次数是常数。每一次随机后,我们需要$O(n)$的时间判断这个数是否为众数,因此期望的时间复杂度为$O(n)$。
计算方法为:当众数恰好占据数组的一半时,第一次随机我们有$\frac{1}{2}$的概率找到众数,如果没有找到,则第二次随机时,也就是第二次找到众数的概率为$\frac{1}{4}$,以此类推。因此期望的次数为$i * \frac{1}{2^i}$的和,可以计算出这个和为2,说明期望的随机次数是常数。每一次随机后,我们需要$O(n)$的时间判断这个数是否为众数,因此期望的时间复杂度为$O(n)$。
空间复杂度:$O(1)$。随机方法只需要常数级别的额外空间。
方法四:分治
思路
如果数a是数组nums的众数,如果将nums分为两部分,那么a必定是至少一部分的众数。
可以用反证法证明这个结论。假设a既不是左半部分的众数,也不是右半部分的众数,那么a出现的次数少于l/2+r/2次,其中l和r分别是左半部分和右半部分的长度。由于l/2+r/2<=(l+r)/2,说明a不是数组nums的众数,因此出现了矛盾。所以这个结论时正确的。
说明我们可以使用分治法解决这个问题:将数组分成左右两个部分,分别求出左半部分的众数a1以及右半部分的众数a2,随后在a1和a2中选出正确的众数。
算法
使用经典的分治算法递归求解,知道所有的子问题都是长度为1的数组,长度为1的子数组中唯一的数显然就是众数,直接返回即可。
如果回溯后某区间长度大于1,将左右子区间的值合并。如果众数相同,这一段区间的众数就确定下来。否则,需要比较两个众数在整个区间内出现的次数来确定该区间的众数。
代码
class Solution:
def majorityElement(self, nums, lo=0, hi=None):
def majority_element_rec(lo, hi):
# basic case;the only element in an array of size 1 is the majority element.
if lo == hi:
return nums[lo]
# recurse on left and right halves of this slice.
mid = (hi - lo) // 2 + lo
left = majority_element_rec(lo, mid)
right = majority_element_rec(mid+1, hi)
# if the two halves agree on the majority element, return it.
if left == right:
return left
# otherwise, count each element and return the 'winner'.
left_count = sum(1 for i in range(lo, hi+1) if nums[i] == left)
right_count = sum(1 for i in range(lo, hi+1) if nums[i] == right)
return left if left_count > right_count else right
return majority_element_rec(0, len(nums)-1)复杂度分析
- 时间复杂度:$O(n\logn)$。函数
majority_element_rec()会求解 2 个长度为$\dfrac{n}{2}$的子问题,并做两遍长度为$n$的线性扫描。因此,分治算法的时间复杂度可以表示为:
根据主定理(百度百科,有条件去看wiki),本题满足第二种情况,所以时间复杂度可以表示为:
- 空间复杂度:$O(\log n)$。尽管分治算法没有直接分配额外的数组空间,但在递归的过程中使用了额外的栈空间。算法每次将数组从中间分成两部分,所以数组长度变为
1之前需要进行$O(\log n)$次递归,即空间复杂度为$O(\log n)$。
方法五:Boyer-Moore投票算法
思路
如果我们把众数记为$+1$,把其他数记为$−1$,将它们全部加起来,显然和大于0,从结果本身我们可以看出众数比其他数多。
算法
Boyer-Moore 算法的本质和方法四中的分治十分类似。我们首先给出 Boyer-Moore 算法的详细步骤:
我们维护一个候选众数
candidate和它出现的次数count。初始时candidate可以为任意值,count为 0;我们遍历数组
nums中的所有元素,对于每个元素x,在判断x之前,如果count的值为0,我们先将x的值赋予candidate,随后我们判断x:- 如果
x与candidate相等,那么计数器count的值增加 1; - 如果
x与candidate不等,那么计数器count的值减少 1。
- 如果
在遍历完成后,
candidate即为整个数组的众数。
我们举一个具体的例子,例如下面的这个数组:
[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
在遍历到数组中的第一个元素以及每个在 | 之后的元素时,`candidate 都会因为 count 的值变为 0 而发生改变。最后一次 candidate 的值从 5 变为 7,也就是这个数组中的众数。
简单的证明见官方题解。
代码
class Sollution:
def majorityElement(self, nums):
count = 0
candidate = None
for num in nums:
if count == 0:
candidate = num
count += (1 if num == candidate else -1)
return candidate大部分借鉴了官方的解题思路,就是会简化一下,加上一点点自己的想法。如果直接扫一遍,就是从脑子里过一遍就没得了。。。记录下来印象会深刻一些。每日一题结束!
参考资料
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!