本文最后更新于:2020年7月14日 晚上
PCA简介
是一种统计方法,通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
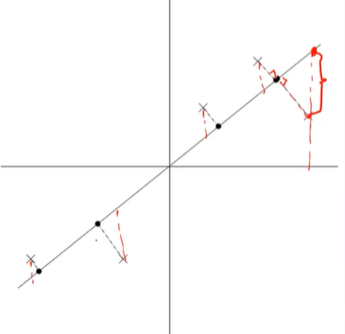
算法本质是找一些投影方向,使得数据在这些投影方向上方差(投影过后的点到原点的平方和)最大。(投影距离小)



线性回归:点到直线的误差值(红线)最小。
PCA:投影距离(垂线方向:黑线)最小。
应用领域:
- 降维
- 高维数据集的探索与可视化
- 数据压缩
- 数据预处理
基于协方差矩阵的特征值分解算法(Eigenvalue Decomposition Algorithm based on Covariance Matrix)
1、均值归一化。计算各个特征均值,然后令$x_j=x_j-u_j$。如果特征在不同数量级上,还需要将其除以标准差,即$x_j=\frac{x_j-u_j}{\sigma_j}$
2、计算协方差矩阵(covariance matrx)$\sum=\frac{1}{m-1}\sum_{i=1}^{m}{X.T*X}$(X为mxn矩阵,m为样本量,n为特征维度)
3、计算协方差矩阵$\sum$的特征向量(eigenvactors):eigenvalues, eigenvectors = np.linalg.eig(sigma)
4、取特征向量u的前k维,得到nxk维度的矩阵,用$U_{reduce}$表示,则降维后的数据为
代码(将二维数据降维为一维数据):
一、导入数据
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
def loaddata():
data = np.loadtxt('data/pca_data.csv',delimiter=',')
return data
X = loaddata()
plt.scatter(X[:,0],X[:,1])
plt.show()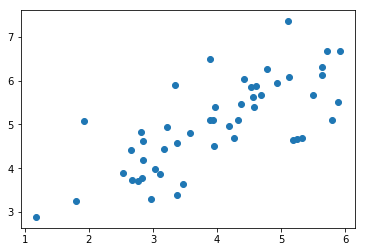
二、特征值归一化及PCA降维
def featureNormalize(X):
mu = np.mean(X,axis=0).reshape(1,-1)
sigma = np.std(X,axis=0,ddof=1).reshape(1,-1)
X = (X-mu)/sigma
return X,mu,sigma
def pca(X, K):
m = len(X)
sigma = np.dot(X.T, X)/(m-1)
# 返回的特征向量需是从大到小排序后的,取前k列。
eigenvalues, eigenvectors = np.linalg.eig(sigma)
index = np.argsort(-eigenvalues) #特征值从大到小排序
eigenvectors = eigenvectors[:,index] #特征向量对应的值
u_reduce = eigenvectors[:,0:K]
return np.dot(X,u_reduce),eigenvectors
X,mu,sigma = featureNormalize(X)
Z,eigenvectors=pca(X,1)
print(Z)输出:
[[ 1.48127391]
[-0.91291229]
[ 1.21208656]
[ 1.62734009]
[ 1.26042409]
[-0.96700223]
[ 1.25605967]
[-2.31794969]
[-0.02968998]
[-0.77386123]
[-0.62532902]
[-0.54724542]
[-0.08878025]
[-0.520569 ]
[ 1.548434 ]
[-1.89684585]
[-0.87788459]
[ 0.94646472]
[-2.30653955]
[-0.4731351 ]
[-2.19518524]
[ 0.38509662]
[-1.76688508]
[ 0.0512347 ]
[ 1.64838858]
[ 0.50302869]
[-1.2246766 ]
[-1.16020771]
[ 0.83375215]
[-0.00686207]
[-0.22565101]
[-1.49788781]
[ 1.3252858 ]
[-0.58656923]
[ 0.67225099]
[-1.33938187]
[ 1.67053477]
[-1.37836539]
[ 2.53419743]
[-0.27570789]
[-0.96695982]
[ 0.8792732 ]
[ 1.28362916]
[-0.97972108]
[ 1.79450473]
[-0.26923019]
[ 3.16088618]
[ 1.20080033]
[ 0.36423084]
[-1.42814204]]三、画图(recover到了两维上??)
def recover(Z, U, K):
U_reduce = U[:,0:K]
X_rec = np.dot(Z,np.transpose(U_reduce))
return X_rec
def plotData(X_origin, X_rec):
plt.scatter(X_origin[:,0], X_origin[:,1])
plt.scatter(X_rec[:,0],X_rec[:,1],c='red')
plt.show()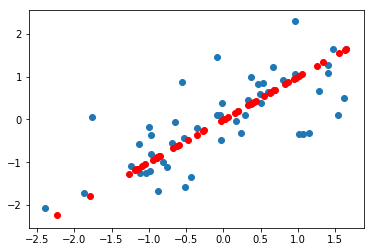
基于数据矩阵的奇异值分解算法(Singular Value Decomposition Algorithm based on Data Matrix)
1、均值归一化。计算各个特征均值,然后令$x_j=x_j-u_j$。如果特征在不同数量级上,还需要将其除以标准差,即$x_j=\frac{x_j-u_j}{\sigma_j}$
2、对数据矩阵进行SVD分解:$u,s,v^T = np.linalg.svd(X,full_matrices=0)$
3、取特征向量$v^T$的前k维,得到kxn维度的矩阵,用$U_{reduce}$表示,则降维后的数据为
解释:
奇异值分解如下式所示:
其中$\sum$特征值矩阵是非常稀疏的,取其特征值前top r列,上式转换为:
(1)式在第2个步骤中分解为$X^{m \times n} \approx u^{m \times n} {\sum}^{n \times n} (v^T)^{n \times n}$,然后根据实际需要,取前r行即可。
代码(将二维数据降维为一维数据):
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
def loaddata():
data = np.loadtxt('data/pca_data.csv',delimiter=',')
return data
X = loaddata() # 和上一个代码一样的数据,就不展示了
def featureNormalize(X):
mu = np.mean(X,axis=0).reshape(1,-1)
sigma = np.std(X,axis=0,ddof=1).reshape(1,-1)
X = (X-mu)/sigma
return X,mu,sigma
def pca(X,K):
u,s,vT = np.linalg.svd(X, full_matrices=0)
return X.dot(vT.T[:,0:K]),u,s,vT
X,mu,sigma = featureNormalize(X)
Z,u,s,vT = pca(X,1)
def recoverData(Z, vT, K):
V_reduce = vT[:,0:K]
X_rec = np.dot(Z,np.transpose(V_reduce))
return X_rec
def plotData(X_orgin,X_rec):
plt.scatter(X_orgin[:,0],X_orgin[:,1])
plt.scatter(X_rec[:, 0], X_rec[:, 1],c='red')
plt.show()
X_rec = recoverData(Z,vT,1)
plotData(X,X_rec)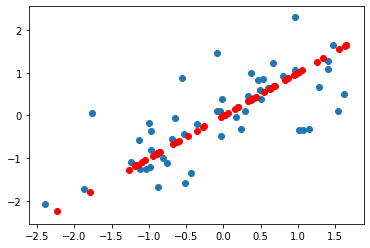
Sklearn实现PCA
1、如何选取主成分个数(How to choose the num of Principal Component)
主成分分析主要是减少投影的平均均方误差,即
(1)
值越小越好(例如:等于0.01,表示原数据99%的信息都保留下来),但此种计算方法耗时大。
(2)
$S_{ii}$是特征值矩阵对角线元素,该值越大越好(如等于0.99,表示元数据99%的信息都保留下来),此种计算方法耗时小。
2、Sklearn实现PCA
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import scipy.io
from sklearn.decomposition import PCA
def loaddata():
data = np.loadtxt('data/pca_data.csv',delimiter=',')
return data
def plotData(X_orgin,X_rec):
plt.scatter(X_orgin[:,0],X_orgin[:,1])
plt.scatter(X_rec[:, 0], X_rec[:, 1],c='red')
plt.show()
X = loaddata()
model = PCA(n_components=1) #定义PCA
Z = model.fit_transform(X) #生成降维后数据
print("主成分个数=",model.n_components)
print("贡献比=",model.explained_variance_ratio_)
print("特征的方差=",model.explained_variance_)
X_rec = model.inverse_transform(Z) #还原数据
plotData(X,X_rec)输出:
主成分个数= 1
贡献比= [0.87062385]
特征的方差= [2.10987818]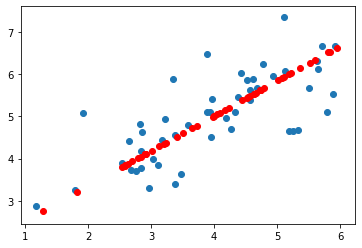
照片压缩
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# 读取照片
img=mpimg.imread("data/xxx.jpg")
# # 显示照片
# plt.imshow(img)
# # 查看照片维度
# print(image.shape) # (800,600,3)
# 把照片转换为二维数组
X = img.reshape(1200,1200)
# 数据标准化
X = StandardScaler().fit_transform(X) # 为了算法快速收敛
# 使用PCA降维
model = PCA(n_components=50)
Z = model.fit_transform(X)
# Z.shape (1200, 50)
print("贡献比=",np.sum(model.explained_variance_ratio_))
# 贡献比= 0.9837087238843197
# model.explained_variance_ratio_.shape (50,)
# 数据还原
X_rec = model.inverse_transform(Z)
X_rec = X_rec.reshape(800,600,3)
# 显示还原后的照片
plt.imshow(X_rec)照片还是不放了~大家可以找网上的照片练练手~
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!