本文最后更新于:2020年7月12日 下午
层次聚类(Hierarchical Clustering)
1、聚合(agglomerative)或自下而上(bottom-up)聚类
2、分裂(divisive)或自上而下(top-down)聚类
AGNES(Agglomerative Nesting):凝聚层次聚类——自下而上
1、构造m个类,每个类包含一个样本
2、计算类与类之间的距离$d_{ij}$,记做矩阵$D=[d_{ij}]_{m \times m}$
3、合并间距最小的两个类
4、若达到聚类数k则退出
5、重新计算类之间的距离$d_{ij}$,重复3
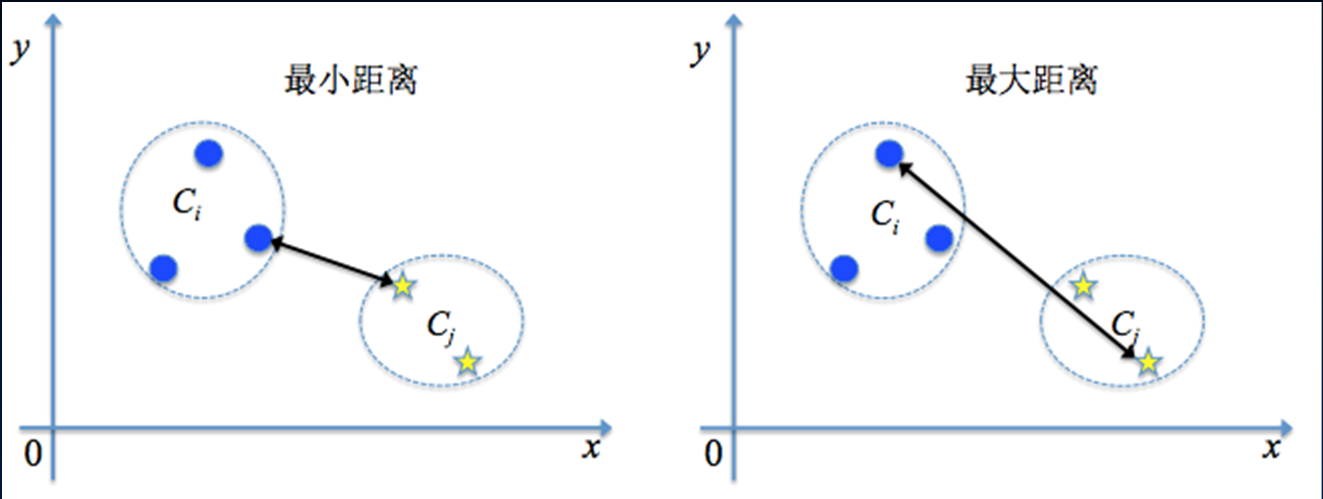
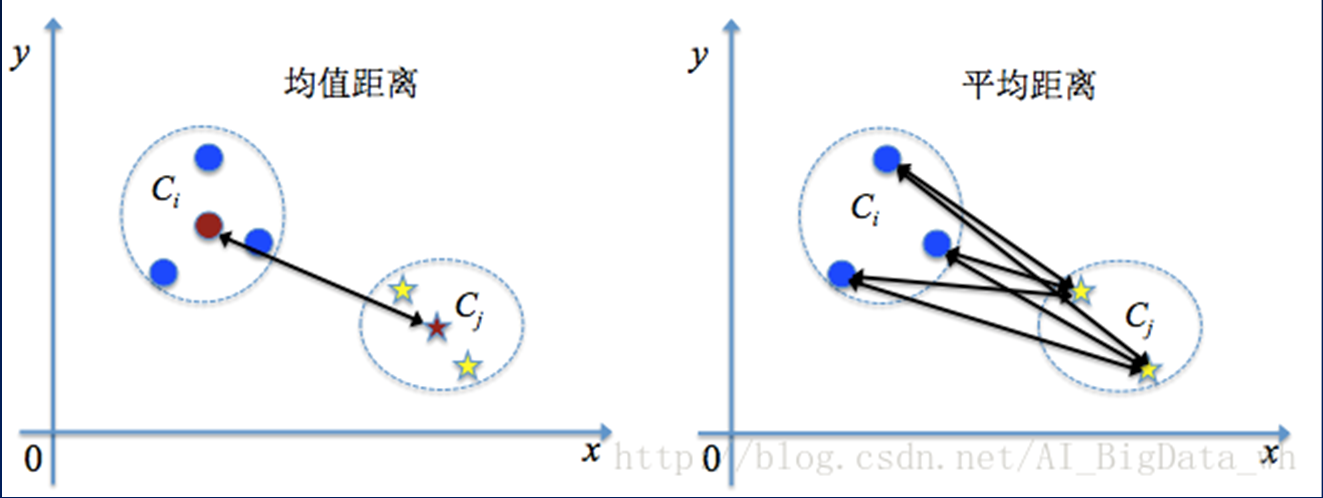
计算类间距离
1、最小距离(单连接,single linkage)
2、最大距离(完全连接,complete linkage)
3、中心/均值距离(计算中心,两个类中心之间的距离)
4、平均距离
代码
import matplotlib.pyplot as plt
import matplotlib as mpl
import scripy.io
import numpy as np
from sklearn.cluster import AgglomerativeClustering
def loaddata():
data = np.loadtxt('data/cluster_data.csv', delimiter=',')
return data
X = loaddata()
# linkage可取值:
# -ward:方差
# -complete:最大距离
# -average:平均距离
# -single:最小距离
model = AgglomerativeClustering(n_clusters=3, affinity='euclidean',linkage='complete')
# AgglomerativeClustering(affinity='euclidean', compute_full_tree='auto',
# connectivity=None, distance_threshold=None,
# linkage='complete', memory=None, n_clusters=3)
model.fit(X)
pirnt('每个样本所属的簇:',model.labels_)
cm_dark = mpl.colors.ListedColormap(['g','r','b'])
plt.scatter(X[:,0],X[:,1], c=model.labels_, cmap=cm_dark, s=20)
plt.show()输出:
每个样本所属的簇: [1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1]
密度聚类(Density-based clustering)
DBSCAN是一种著名的密度聚类方法,给定参数$(\varepsilon,Minpts)$
1、$\varepsilon$领域
2、核心对象(Core object)
3、密度直达(directly density-reachable)
4、密度可达(density-reachable)
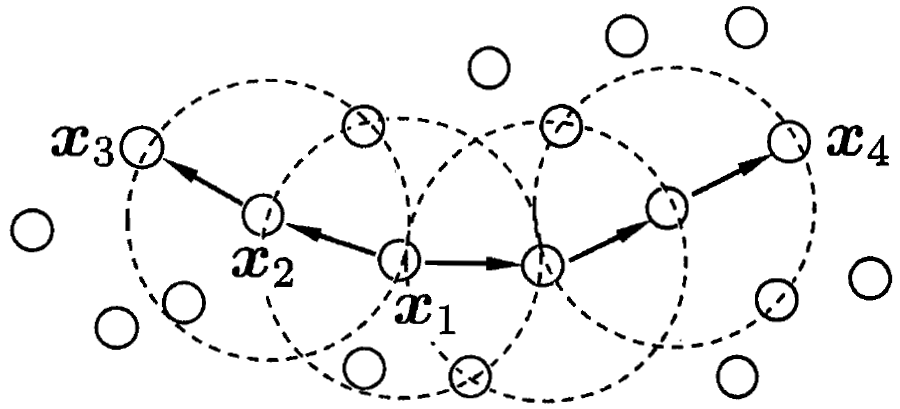
若$minPts=3$,则$x_1,x_2$等都是核心对象
$x_2$由$x_1$密度直达,$x_3$由$x_1$密度可达
密度聚类算法过程:
1、首先设置$(\varepsilon,Minpts)$参数
2、确定核心对象,假设为$\Omega ={x^{(3)},x^{(5)},x^{(6)},x^{(8)},x^{(9)},x^{(13)},x^{(14)},x^{(18)} ,x^{(19)} ,x^{(24)} ,x^{(25)},x^{(28)},x^{(29)}}$
3、从$\Omega$中随机选取一个核心对象作为种子(假设为$x^{(8)}$),找出由它密度可达的所有样本,构成一个聚类簇,假设第一个聚类簇为$C_1 = \{ x^{(6)},x^{(7)},x^{(8)},x^{(10)},x^{(12)},x^{(18)},x^{(19)},x^{(20)},x^{(23)} \}$
4、从$\Omega$中去除$C_1$中包含的核心对象后,$\Omega ={x^{(3)},x^{(5)},x^{(9)},x^{(13)},x^{(14)},x^{(24)} ,x^{(25)},x^{(28)},x^{(29)}}$,重复3直至$\Omega$为空。
代码
import matplotlib.pyplot as plt
import matplotlib as mpl
import scripy.io
import numpy as np
from sklearn.cluster import DBSCAN
def loaddata():
data = np.loadtxt('data/cluster_data.csv', delimiter=',')
return data
X = loaddata()
model = DBSCAN(eps=0.5, min_samples=5, metric='euclidean')
model.fit(X)
print('每个样本所属的簇:', model.labels_)
cm_dark = mpl.colors.ListedColormap(['g','r','b','c'])
plt.scatter(X[:,0], X[:,1], c=model.labels_, cmap=cm_dark, s=20)输出(-1类为离群点):
每个样本所属的簇: [ 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 -1
0 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 -1 2 -1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 -1 -1 1 1 1 1 1 1 1 1 1 1 1 1 -1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 0]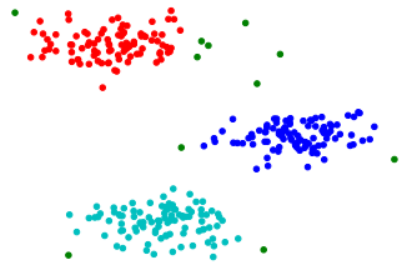
高斯混合模型(Gaussian Mixed Model)
高斯模型($x$为单变量):
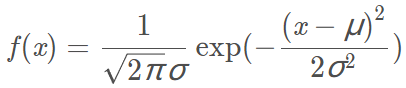
均值为0,方差为1的概率密度函数:
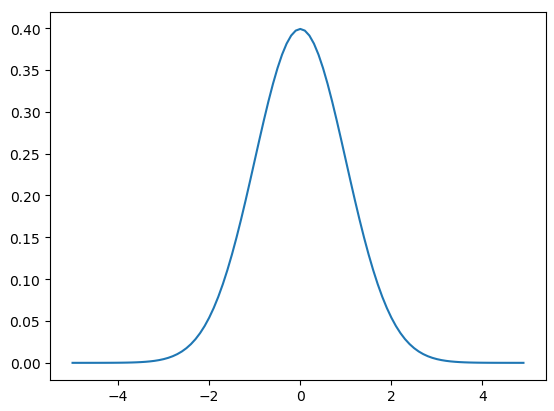
高斯模型($X$为多变量,维度为$n$,$d=n$,$\sum$为$X$的协方差矩阵,大小为$n \times n$,$\overrightarrow{u}=(u_1,u_2,\ldots,u_n)$):
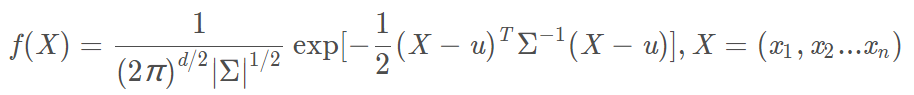
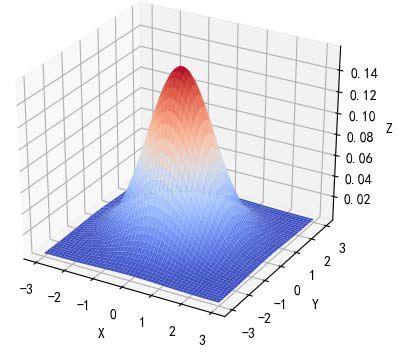
为什么要用高斯混合模型:
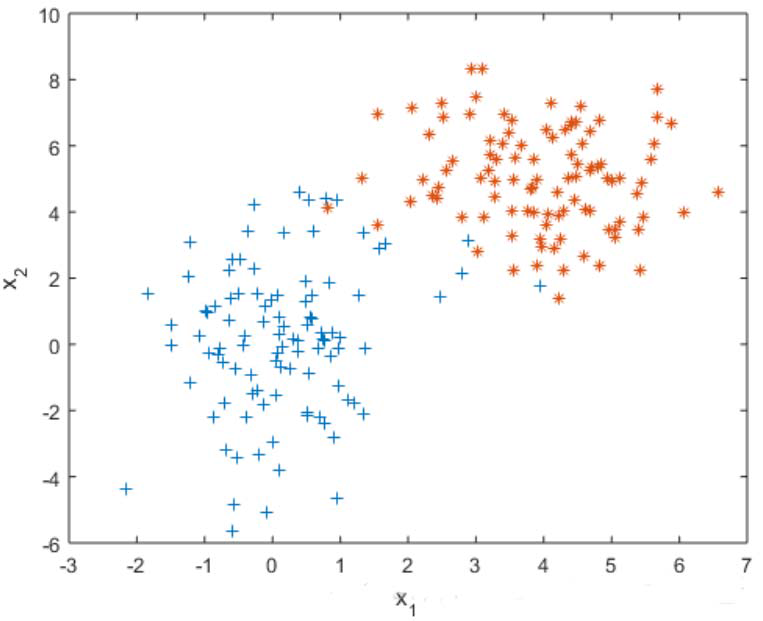
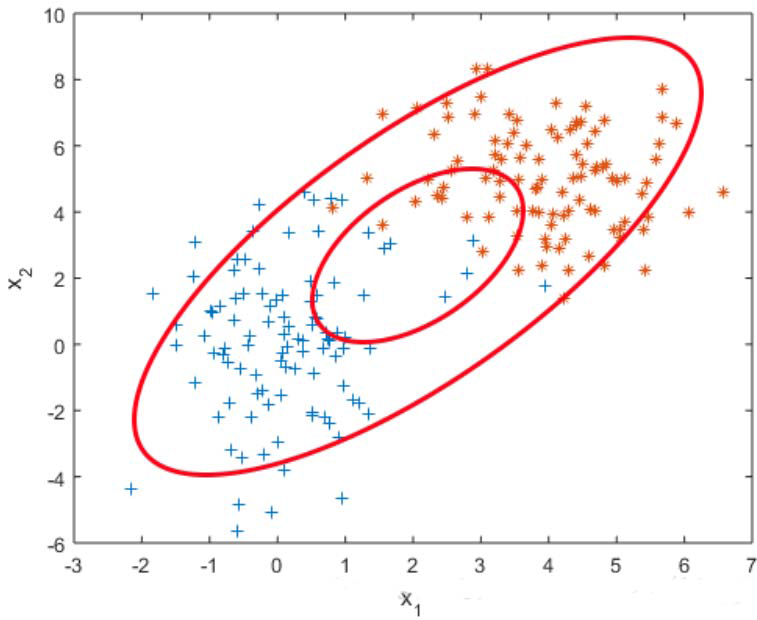
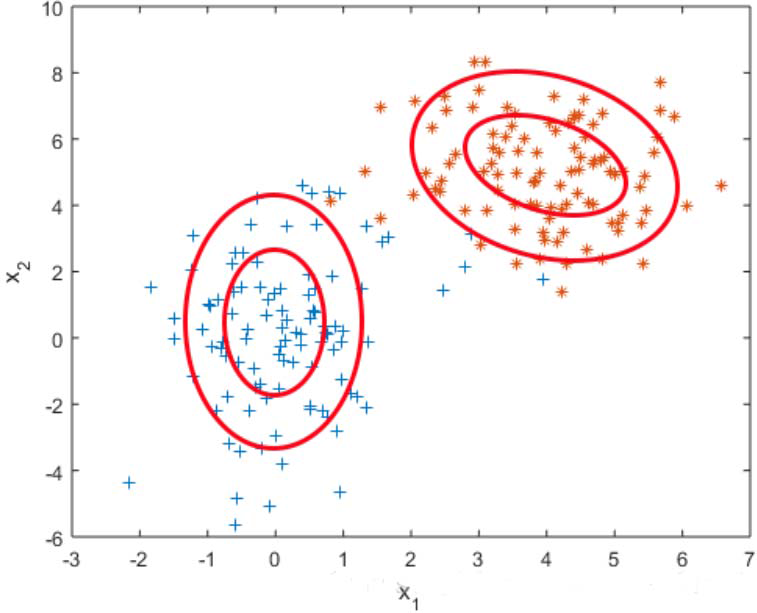
用单变量高斯模型无法拟合上图所示分布(两类数据的分布),用高斯混合模型可以较好拟合。
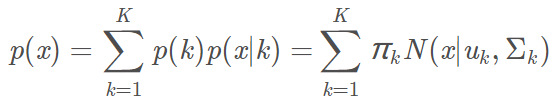
其中 $k$ 为类别数,$\pi_k$为第 $k$ 个高斯模型的权重,$N(x|u_k,\sum_k)$为第 $k$ 个高斯模型,$u_k,\sum_k$是第 $k$ 个高斯模型的参数(均值向量,协方差矩阵)。
高斯混合模型参数计算
第 $i$ 个样本属于第k个类别的概率:
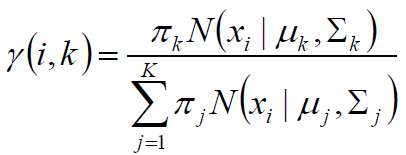
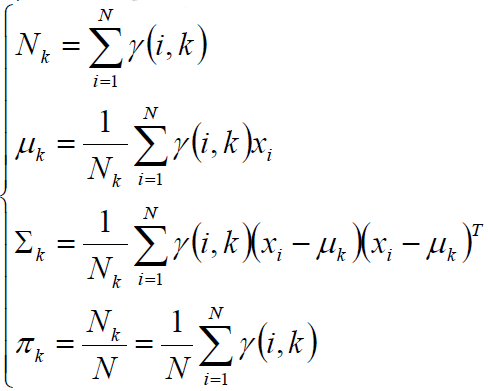
交替更新,直至收敛稳定。
手工代码
一、生成数据进行实验
import numpy as np
import matplotlib.pyplot as plt
# 生成一些数据进行实验
# 1.生成均值为1.71,标准差为0.056的男生身高数据
np.random.seed(0)
mu_m = 1.71 # 期望
sigma_m = 0.056 # 标准差
num_m = 10000 # 数据个数为10000
random_data_m = np.random.normal(mu_m, sigma_m, num_m) #生成数据
y_m = np.ones(num_m) # 生成标签
# 2.生成均值为1.58,标准差为0.051的女生身高数据
np.random.seed(0)
mu_w = 1.58 #期望
sigma_w = 0.051 #标准差数据
num_w = 10000 #个数为10000
rand_data_w = np.random.normal(mu_w, sigma_w, num_w)#生成数据
y_w = np.zeros(num_m)#生成标签
# 3.把男生数据和女生数据合在一起
data = np.append(rand_data_m,rand_data_w)
data = data.reshape(-1,1)
y = np.append(y_m,y_w)
print(data)
print(y)输出:
[[1.80878693]
[1.7324088 ]
[1.76480933]
...
[1.60636048]
[1.57832104]
[1.64620368]]
[1. 1. 1. ... 0. 0. 0.]二、高斯混合模型拟合数据
from scipy.stats import multivariate_normal
num_iter = 1000
n, d = data.shape
#初始化参数
mu1 = data.min(axis=0)
mu2 = data.max(axis=0)
sigma1 = np.identity(d)
sigma2 = np.identity(d)
pi = 0.5
for i in range(num_iter):
#计算gamma
norm1 = multivariate_normal(mu1, sigma1)
norm2 = multivariate_normal(mu2, sigma2)
tau1 = pi * norm1.pdf(data)
# print('tau1', tau1)
tau2 = (1 - pi) * norm2.pdf(data)
gamma = tau1 / (tau1 + tau2)
# print('gamma',gamma)
#计算mu1
mu1 = np.dot(gamma, data) / np.sum(gamma)
# print("第%d iter: mul=%f" % (i, mu1))
#计算mu2
mu2 = np.dot(1-gamma, data) / np.sum(1 - gamma)
#计算sigma1
sigma1 = np.dot(gamma * (data-mu1).T, (data - mu1) ) / np.sum(gamma)
# print("第%d iter: sigma1=%f" %(i,sigma1))
#计算sigmal2
sigma2 = np.dot((1-gamma) * (data-mu2).T, (data - mu2)) / np.sum(1 - gamma)
#计算pi
# print("第%d iter: sigma1=%f" %(i,sigma2))
pi = np.sum(gamma)/n
print(u'类别概率:\t', pi)
print(u'均值:\t', mu1, mu2)
print(u'方差:\n', sigma1, '\n\n', sigma2, '\n')输出:
类别概率: 0.4873884639284559
均值: [1.57749047] [1.70726384]
方差:
[[0.00244834]]
[[0.00315184]]sklean实现高斯混合模型
一、生成实验数据
import numpy as np
import matplotlib.pyplot as plt
# 生成一些数据进行实验
# 1.生成均值为1.71,标准差为0.056的男生身高数据
np.random.seed(0)
mu_m = 1.71 # 期望
sigma_m = 0.056 # 标准差
num_m = 10000 # 数据个数为10000
random_data_m = np.random.normal(mu_m, sigma_m, num_m) #生成数据
y_m = np.ones(num_m) # 生成标签
# 2.生成均值为1.58,标准差为0.051的女生身高数据
np.random.seed(0)
mu_w = 1.58 #期望
sigma_w = 0.051 #标准差数据
num_w = 10000 #个数为10000
rand_data_w = np.random.normal(mu_w, sigma_w, num_w)#生成数据
y_w = np.zeros(num_m)#生成标签
# 3.把男生数据和女生数据合在一起
data = np.append(rand_data_m,rand_data_w)
data = data.reshape(-1,1)
y = np.append(y_m,y_w)
print(data)
print(y)二、sklean实现高斯混合模型拟合数据
from sklearn.mixture import GaussianMixture
# n_components:类别数 max_iter:迭代次数
g = GaussianMixture(n_components=2, covariance_type='full', tol=1e-6, max_iter=1000)
g.fit(data)
print(u'类别概率:\t', g.weights_[0])
print(u'类别概率:\t', g.weights_[1])
print(u'均值:\n', g.means_, '\n')
print(u'方差:\n', g.covariances_, '\n')输出:
类别概率: 0.4996454306546242
类别概率: 0.5003545693453813
均值:
[[1.57895001]
[1.70898537]]
方差:
[[[0.00251652]]
[[0.00306363]]]测试准确率:
from sklearn.metrics import accuracy_score
y_hat = g.predict(data)
print(accuracy_score(y,y_hat))输出(重叠区域不好判断):
0.8891对亚洲足球队进行聚类分析
代码
导入数据
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler # 标准归一化
df = pd.read_csv('data/football_team_data.csv', index_col='国家')
print(df)输出:
2019国际排名 2018世界杯 2015亚洲杯
国家
中国 73 40 7
日本 60 15 5
韩国 61 19 2
伊朗 34 18 6
沙特 67 26 10
伊拉克 91 40 4
卡塔尔 101 40 13
阿联酋 81 40 6
乌兹别克斯坦 88 40 8
泰国 122 40 17
越南 102 50 17
阿曼 87 50 12
巴林 116 50 11
朝鲜 110 50 14
印尼 164 50 17
澳洲 40 30 1
叙利亚 76 40 17
约旦 118 50 9
科威特 160 50 15
巴勒斯坦 96 50 16取出数字列
X = df.values
print(X)输出:
array([[ 73, 40, 7],
[ 60, 15, 5],
[ 61, 19, 2],
[ 34, 18, 6],
[ 67, 26, 10],
[ 91, 40, 4],
[101, 40, 13],
[ 81, 40, 6],
[ 88, 40, 8],
[122, 40, 17],
[102, 50, 17],
[ 87, 50, 12],
[116, 50, 11],
[110, 50, 14],
[164, 50, 17],
[ 40, 30, 1],
[ 76, 40, 17],
[118, 50, 9],
[160, 50, 15],
[ 96, 50, 16]], dtype=int64)X = StandardScaler().fit_transform(X)
X输出:
array([[-0.5842676 , 0.05223517, -0.64677721],
[-0.97679881, -2.12423024, -1.03291285],
[-0.9466041 , -1.77599577, -1.61211632],
[-1.76186121, -1.86305439, -0.83984503],
[-0.76543585, -1.16658546, -0.06757374],
[-0.04076286, 0.05223517, -1.22598067],
[ 0.26118422, 0.05223517, 0.51162973],
[-0.34270994, 0.05223517, -0.83984503],
[-0.13134698, 0.05223517, -0.45370938],
[ 0.89527309, 0.05223517, 1.28390102],
[ 0.29137893, 0.92282133, 1.28390102],
[-0.16154169, 0.92282133, 0.31856191],
[ 0.71410485, 0.92282133, 0.12549408],
[ 0.5329366 , 0.92282133, 0.70469755],
[ 2.16345083, 0.92282133, 1.28390102],
[-1.58069297, -0.81835099, -1.80518414],
[-0.49368348, 0.05223517, 1.28390102],
[ 0.77449426, 0.92282133, -0.26064156],
[ 2.042672 , 0.92282133, 0.89776537],
[ 0.11021068, 0.92282133, 1.0908332 ]])使用KMeans聚合数据
model = KMeans(n_clusters=3, max_iter=10)
model.fit(X)
#KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=10,
# n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
# random_state=None, tol=0.0001, verbose=0)
df["聚类结果"] = model.labels_
print(df)输出:
2019国际排名 2018世界杯 2015亚洲杯 聚类结果
国家
中国 73 40 7 2
日本 60 15 5 0
韩国 61 19 2 0
伊朗 34 18 6 0
沙特 67 26 10 0
伊拉克 91 40 4 2
卡塔尔 101 40 13 1
阿联酋 81 40 6 2
乌兹别克斯坦 88 40 8 2
泰国 122 40 17 1
越南 102 50 17 1
阿曼 87 50 12 1
巴林 116 50 11 1
朝鲜 110 50 14 1
印尼 164 50 17 1
澳洲 40 30 1 0
叙利亚 76 40 17 1
约旦 118 50 9 1
科威特 160 50 15 1
巴勒斯坦 96 50 16 1根据结果看出,这些国家分为了三类,结合数据进行分析,亚洲足球队强弱顺序依次是0,2,1.
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!