集成学习(Ensemble Learning introduction)

如果聚合一组预测器(比如分类器或回归器)的预测，得到的预测结果也比最好的单个预测器要好。这样的一组预测器，我们称为集成。这种技术，也被称为集成学习，而一个集成学习的算法则被称为集成方法。

• voting(投票)
• Bagging
  • 随机森林(RandomForest)
• Boosting
  • AdaBoost
  • 提升树
  • XGboost
• stacking

voting(投票)

1、硬投票分类器(Hard Voting)

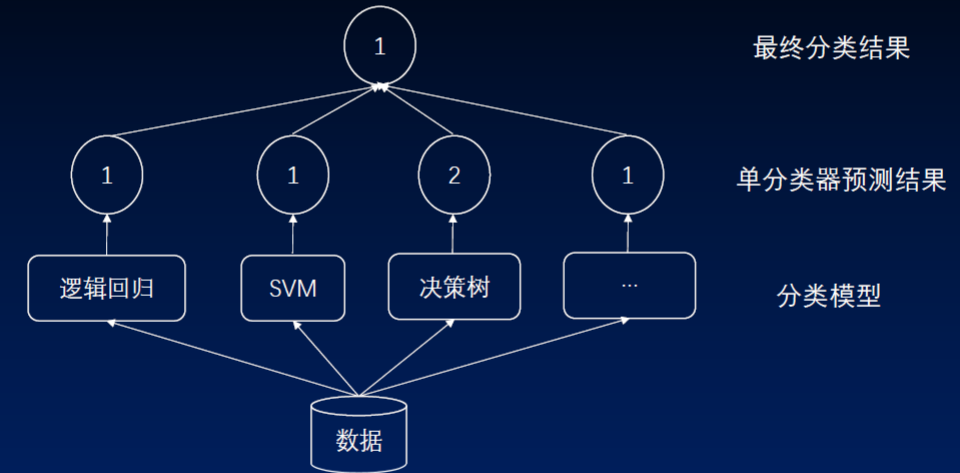
分类结果是01分类，即选择一种结果(跟hard label类似)。

2、软投票分类器(Soft Voting)
分类器能够估算出类别的概率。把概率取平均，取平均概率最高的类别作为预测标签(跟soft label类似)。被称为软投票法。通常来说比硬投票法表现更优，因为它给予那些高度自信的投票更高的权重。

硬投票表决(sklearn代码简单实现)：

from sklearn.ensemble import VotingClassifier

from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC

from sklearn.metrics import accuracy_score
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# 使用Sklearn中moon数据集
X,y = make_moons(n_samples=7000,noise=0.1)
plt.scatter(X[:,0],X[:,1])

# 数据集分割
X_train, X_test, y_train, y_test = train_test_split(X, y , test_size=0.25, random_state=42)
# 定义三个基分类器
# -逻辑回归
# -决策树
# -SVM
lr = LogisticRegression()
dt = DecisionTreeClassifier()
svm = SVC()
# 定义投票分类器
voting = VotingClassifier(
    estimators=[('lr',lr),('dt',dt),('svm',svm)],
    voting='hard'
)
# 输出各个分类器的准确率
for clf in (lr,dt,svm,voting):
    clf.fit(X_train,y_train)
    y_hat = clf.predict(X_test)
    print(clf.__class__.__name__,'=',accuracy_score(y_test,y_hat))

输出：

LogisticRegression = 0.8862857142857142
DecisionTreeClassifier = 0.996
SVC = 0.9988571428571429
VotingClassifier = 0.9977142857142857

软投票表决(跟上面的代码只有一些些不同)：

# 数据集加载是一致的
# 定义三个基分类器
lr = LogisticRegression()
dt = DecisionTreeClassifier()
svm = SVC(probability=True) # probability设置为True，概率形式的预测结果输入到votingClassifier中
# 定义投票分类器
voting = VotingClassifier(
    estimators=[('lr',lr),('rf',dt),('svc',svm)],
    voting='soft' # 设置为soft
)
# 输出各个分类器的准确率
for clf in (lr,dt,svm,voting):
    clf.fit(X_train,y_train)
    y_hat = clf.predict(X_test)
    print(clf.__class__.__name__,'=',accuracy_score(y_test,y_hat))

输出：

LogisticRegression = 0.88
DecisionTreeClassifier = 0.9994285714285714
SVC = 0.9994285714285714
VotingClassifier = 0.9994285714285714

Bagging(并行)

bagging和pasting
每个预测器使用的算法相同，但是在不同的训练集(随机子集)上进行训练。采样时如果将样本放回，这汇总方法叫做bagging(bootstrap aggregating，自举汇聚法)。采样时样本不放回，这种方法叫做pasting。
(实际应用中bagging更加常用。这里就着重介绍bagging)

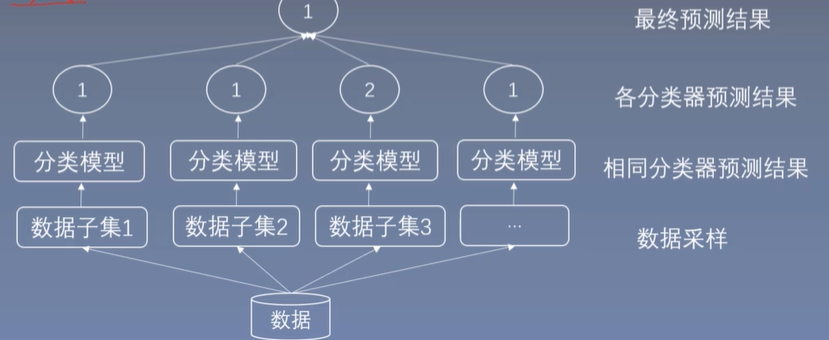
随机森林(Random Forest)

随机森林是决策树的集成，通常用bagging(有时也可能是pasting)方法训练。除了先构建一个BaggingClassifier然后将结果传输到DecisionTreeClassifier，还有一种方法就是使用RandomForestClassifier类。

大概有63.2%样本会被抽到，用作训练集。未抽到的37.8%样本(out of bag简称oob)作为测试集。
证明：假设进行N次抽样，未抽到的概率为 $1-(1-\frac{1}{N})^N=1-[(1+\frac{1}{-N})^{-N}]^{-1}$，当N趋于无穷大时，上式趋于$1-e^{-1}=63.2\%$。

代码：

from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
import numpy as np
iris = load_iris()
X = iris.data
y = iris.target
# bootstrap = True 为bagging，bootstrap=False为pasting
# max_samples设置为整数表示的就是采样的样本数，设置为浮点数表示的是max_samples*x.shape[0]
# oob_score=True表示未抽到的样本作为测试集
# n_estimators基本分类器的数量
bag_clf = BaggingClassifier(
    SVC(),
    n_estimators=500, max_samples=1.0, bootstrap=True, n_jobs=-1 
    ,oob_score=True
)
bag_clf.fit(X,y)
# oob_score默认为False时进行下列预测
# y_hat = bag_clf.predict(X)
# print(bag_clf.__class__.__name__,'=',accuracy_score(y,y_hat))
# BaggingClassifier = 0.9733333333333334
print(bag_clf.oob_score_)

输出：

0.9666666666666667

如果基本分类器是决策树，那么集成后的分类器就是随机森林

bag_clf = BaggingClassifier(
    DecisionTreeClassifier(splitter="random", max_leaf_nodes=16),
    n_estimators=500, max_samples=1.0, bootstrap=True, n_jobs=-1
)
bag_clf.fit(X,y)
y_hat = bag_clf.predict(X)
print(bag_clf.__class__.__name__,'=',accuracy_score(y,y_hat))

输出：

BaggingClassifier = 1.0

Sklearn也提供了直接实现随机森林的API

rnd_clf = RandomForestClassifier(n_estimators=500, n_jobs=-1)
rnd_clf.fit(X, y)
print(rnd_clf.__class__.__name__, '=', accuracy_score(y, y_hat))

输出：

RandomForestClassifier = 1.0

Boosting(串行)

将几个弱学习器结合成一个强学习器的集成方法。大多数提升法的总体思想是循环训练预测器，每一次都对其前序做出一些改正。

• AdaBoost
• GBDT
• XGBoost

AdaBoost基本原理

• AdaBoost：从弱学习算法出发，反复学习得到一系列弱分类器(又称基本分类器)，然后组合这些弱分类器构成一个强分类器。

• 要解决的两个问题：

  1、每一轮如何改变训练数据的权值或概率分布：提高那些被前一轮错误分类样本的权值，降低那些被正确分类样本的权值。
  2、如何将弱分类器组合成强分类器：加大分类误差小的弱分类器权值，减小分类误差率大的弱分类器权值。

AdaBoost算法流程

（1）初始化训练数据权值分布 $D_1=(w_{11},\ldots,w_{1i},\ldots,w_{1m}),\quad w_{1i}=\frac{1}{m}$
（2）对于每一轮训练t=1,2,…,T
  (a)使用具有权值分布Dt的训练数据集进行学习，得到基本分类器$G_t(x)$
  (b)计算$G_t(x)$在训练数据集上的分类误差率：

$$e_t=\sum_{i=1}^{m}P(G_t(x^{(i)})\neq y^{(i)})=\sum_{i=1}^{m}w_{ti}I(G_t(x^{(i)}) \neq y^{(i)})$$

  (c)计算$G_t(x)$的权重系数 $\alpha_t = \frac{1}{2}\log{\frac{1-e_t}{e_t}}$
  (d)更新训练数据集的权重分布 $D_{t+1}=(w_{t+1,1},\ldots,w_{t+1,i},\ldots,w_{t+1,m})$
（3）构建基本分类器的线性组合 $w_{t+1,i}=\frac{w_{ti}}{Z_t}\exp{(-\alpha_t y^{(i)} G_t(x^{(i)}))}$，其中$Z_t$是归一化因子，$Z_t=\sum_{i=1}^{m}w_{ti}\exp{(-\alpha_t y^{(i)}) G_t(x^{(i)})}$
   $f(x)=\sum_{i=1}^{T} \alpha_t G_t(x)$ 得到最终分类器 $G(x)=sign(f(x))=sign(\sum_{t=1}^{T} \alpha_t G_t(x))$

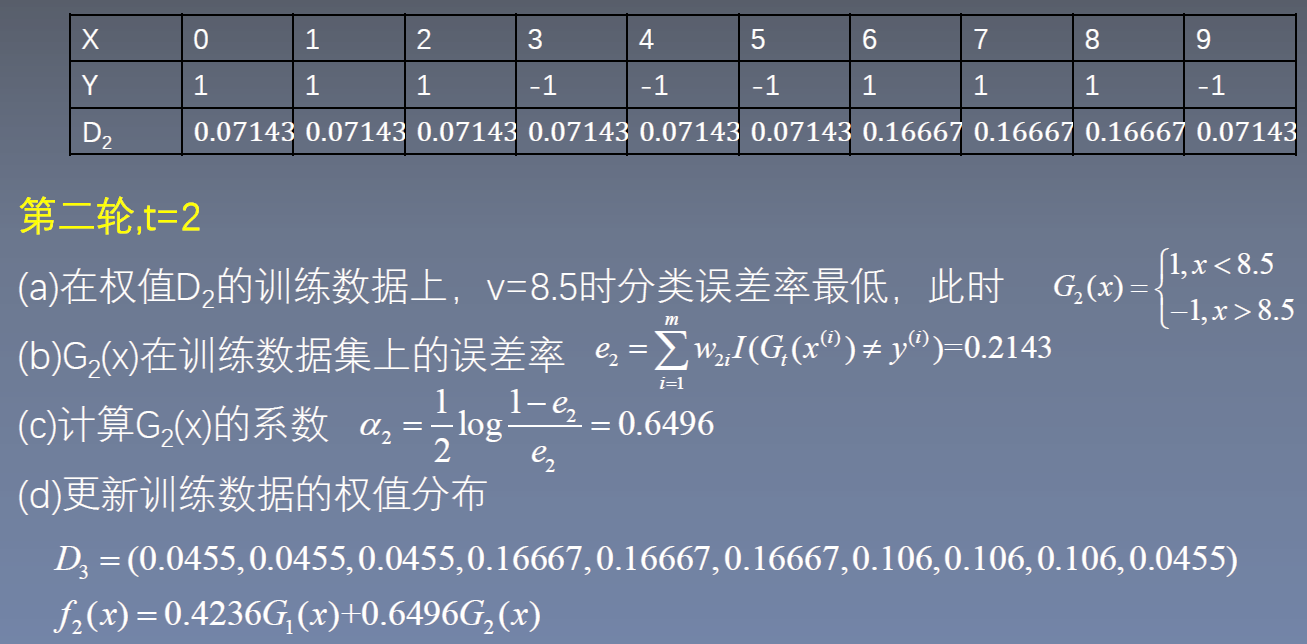
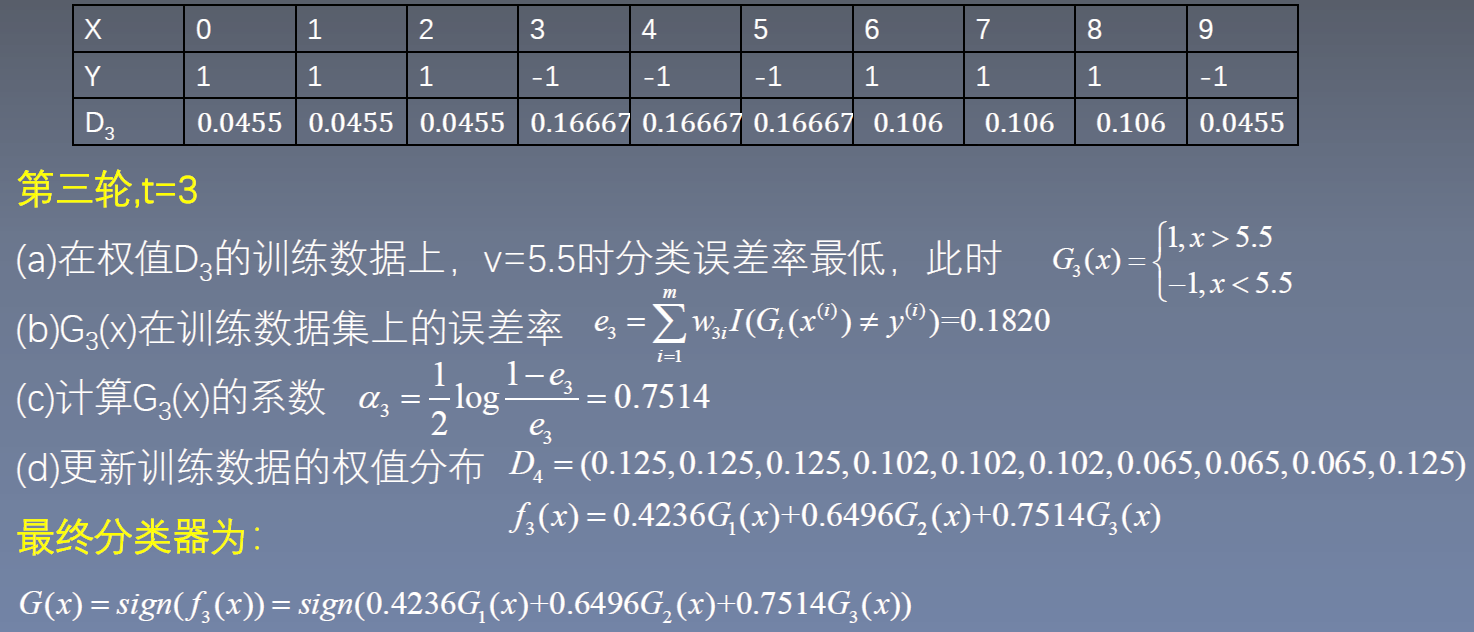
AdaBoost代码(Sklearn实现)

代码(参数明细见scikit-learn Adaboost类库使用小结)：

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import numpy as np
data = np.loadtxt('data/wine.data',delimiter=',')
X = data[:,1:]
y = data[:,0:1]

# 对于决策树而言，归一化作用不明显，对于逻辑回归而言，归一化是比较有用的~
# from sklearn.preprocessing import StandardScaler
# X = StandardScaler().fit_transform(X)
# from sklearn.linear_model import LogisticRegression
# rf = LogisticRegression()

X_train,X_test,y_train,y_test = train_test_split(X,y.ravel(),train_size=0.8,random_state=0)
# 定义弱(基)分类器
rf = DecisionTreeClassifier()
# 定义AdaBoost分类器
model = AdaBoostClassifier(base_estimator=rf,n_estimators=50,algorithm="SAMME.R", learning_rate=0.5)
model.fit(X_train,y_train)
#AdaBoostClassifier(algorithm='SAMME.R',
#                   base_estimator=DecisionTreeClassifier(ccp_alpha=0.0,
#                                                         class_weight=None,
#                                                         criterion='gini',
#                                                         max_depth=None,
#                                                         max_features=None,
#                                                         max_leaf_nodes=None,
#                                                         min_impurity_decrease=0.0,
#                                                         min_impurity_split=None,
#                                                         min_samples_leaf=1,
#                                                         min_samples_split=2,
#                                                         min_weight_fraction_leaf=0.0,
#                                                         presort='deprecated',
#                                                         random_state=None,
#                                                         splitter='best'),
#                   learning_rate=0.5, n_estimators=50, random_state=None)
y_train_hat = model.predict(X_train)
print("train accuarcy:",accuracy_score(y_train,y_train_hat))
y_test_hat = model.predict(X_test)
print("test accuarcy:", accuracy_score(y_test, y_test_hat))

输出：

train accuarcy: 1.0
test accuarcy: 0.9722222222222222

---

梯度提升(Gradient Boosting Tree)

与AdaBoost类似，梯度提升也是逐步在集成中添加预测器，与AdaBoost类似，梯度提升也是在继承中添加预测器，每一个都对其前序做出改正。不同之处在于，它不是像AdaBoost那样在每个迭代中调整实例权重，而是让新的预测器针对前一个预测器的残差进行拟合。

提升树种每一颗树学的是之前所有树结论累积的残差。残差就是真实值和预测值的差值。如A的真实年龄是18，第一棵树预测年龄是12岁，则残差值为6.接下来在第二颗树把A的年龄当初6岁去学习，如果第二棵树能把A分到6岁的叶子节点，那累加两颗树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树把A的年龄当成1岁，继续学。最后，所有树的累加值就是最终预测值。
提升树算法
（1）初始化$f_0(x)=0$
（2）对m=1,2,…,M
  (a) 计算残差 $r_{mi}=y_i-f_{m-1}(x_i)$
  (b) 拟合残差 $r_{mi}$ 学习一个回归树 $T(x;\Theta_m)$
  (c) 更新 $f_m(x)=f_{m-1}(x)+T(x;\Theta_m)$
（3）得到提升树 $f_M(x)=\sum_{i=1}^{M}T(x;\Theta_m)$

代码(预测一维数据的结果)：

from sklearn.tree import DecisionTreeRegressor
import numpy as np
from sklearn.ensemble import GradientBoostingRegressor
import matplotlib.pyplot as plt
def loaddata():
    data = np.loadtxt('data/data.txt',delimiter=',')
    n = data.shape[1]-1 #特征数
    X = data[:,0:n]
    y = data[:,-1].reshape(-1,1)
    return X,y
X,y = loaddata()
plt.scatter(X,y)

1）根据算法原理手动实现(使用决策树回归DesicionTreeRegressor)

# 1、定义第一课树(最大深度设定为5)，并进行训练
tree_reg1 = DecisionTreeRegressor(max_depth=5)
tree_reg1.fit(X, y)
#DecisionTreeRegressor(criterion='mse', max_depth=5, max_features=None,
#                      max_leaf_nodes=None, min_impurity_decrease=0.0,
#                      min_impurity_split=None, min_samples_leaf=1,
#                      min_samples_split=2, min_weight_fraction_leaf=0.0,
#                      presort=False, random_state=None, splitter='best')
# 2、计算残差，并把残差当做目标值训练第二棵树(最大深度设定为5)
y2 = y - tree_reg1.predict(X).reshape(-1,1)
tree_reg2 = DecisionTreeRegressor(max_depth=5)
tree_reg2.fit(X, y2)
# 3、继续计算残差，并把残差当做目标值训练第三棵树(最大深度设定为5)
y3 = y2 - tree_reg2.predict(X).reshape(-1,1)
tree_reg3 = DecisionTreeRegressor(max_depth=5)
tree_reg3.fit(X, y3)
# 4、测试
# 取训练集前5条数据，并对前5条数据做预测
X_new = X[0:5,]
y_pred = sum(tree.predict(X_new) for tree in (tree_reg1, tree_reg2, tree_reg3))
print(y_pred)

输出;

[17.61560196  9.15380196 12.831       4.57199973  6.68971688]

2）直接使用sklearn提供的GradientBoostingRegressor

gbrt = GradientBoostingRegressor(max_depth=5, n_estimators=3, learning_rate=1.0)
gbrt.fit(X, y)
print(gbrt.predict(X_new))

输出：

[17.61560196  9.15380196 12.831       4.57199973  6.68971688]

梯度提升树(Gradient Boosting Tree)

上例中使用的平方损失：$L(y, f_t(x))=\frac{1}{2}(y-f_t(x))^2$
其负梯度为：$-\frac{\partial L(y,f_t(x))}{\partial f_t(x)}=y-f_t(x)$该负梯度就是残差。

• 平方损失拟合残差值
• 非平方损失拟合负梯度值

GBDT：其关键是利用损失函数的负梯度作为提升树算法中要拟合的值。

XGBoost

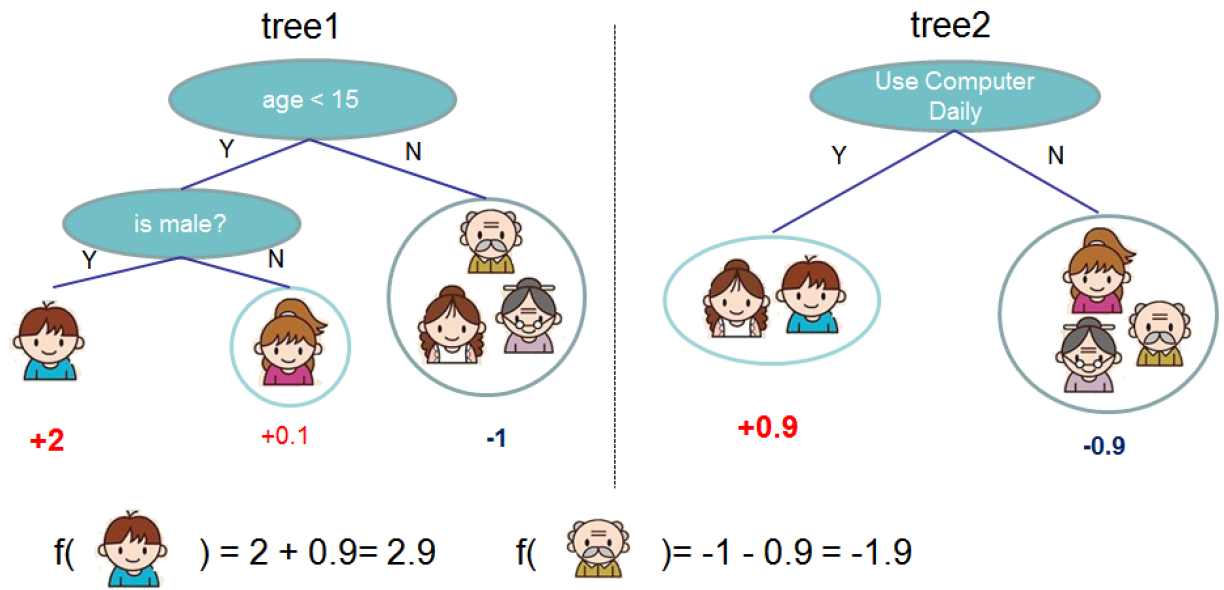
q表示树结构，q把每一个样本点x映射到某一个叶子节点。
T是叶子节点的数量
w是叶子节点的权值(实际就是预测值)
$f_k$表示第k个树，该树的结构由q表示，预测值由w表示。
预测值表示为：

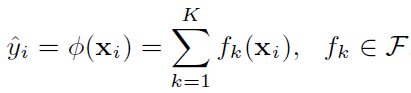
或：

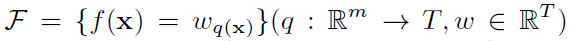
XGBoost损失函数(Loss function of XGBoost)

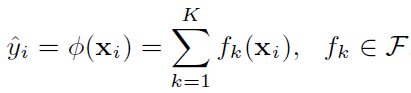
假设损失函数是平方损失，则初值可取所有样本的平均数。

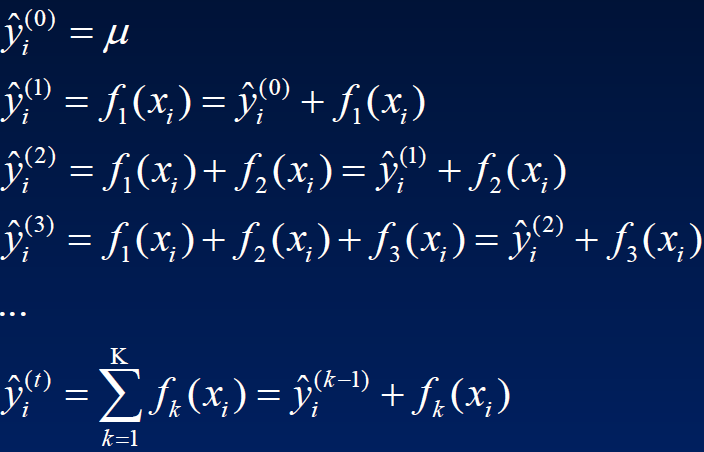
因此损失函数可写为：

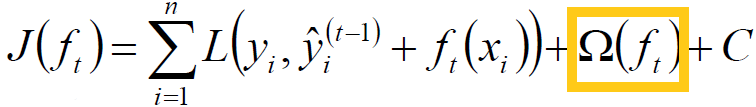
橙框中为正则项，C为常数项。

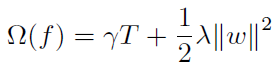
例子：

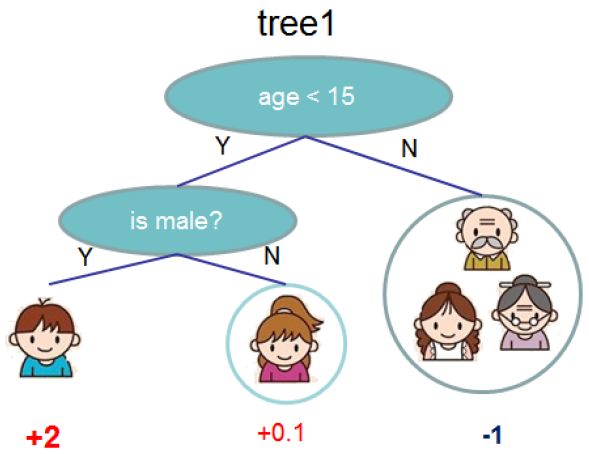
其中$\Omega=\gamma \times 3 + \frac{1}{2} \lambda (4+0.01 + 1)$

XGBoost求解(XGBoost solution)

目标函数：

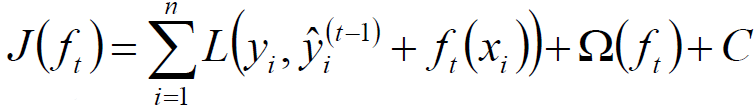
根据Taylor公式：

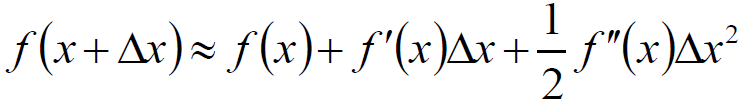
令：

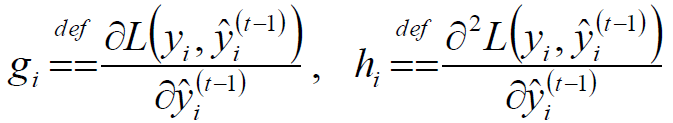
得：

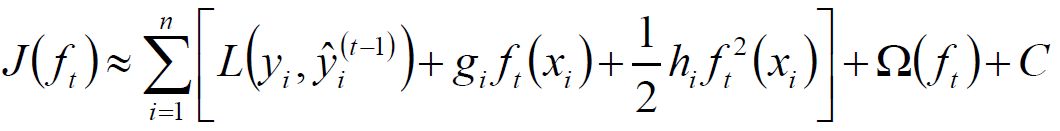
对上式求解：

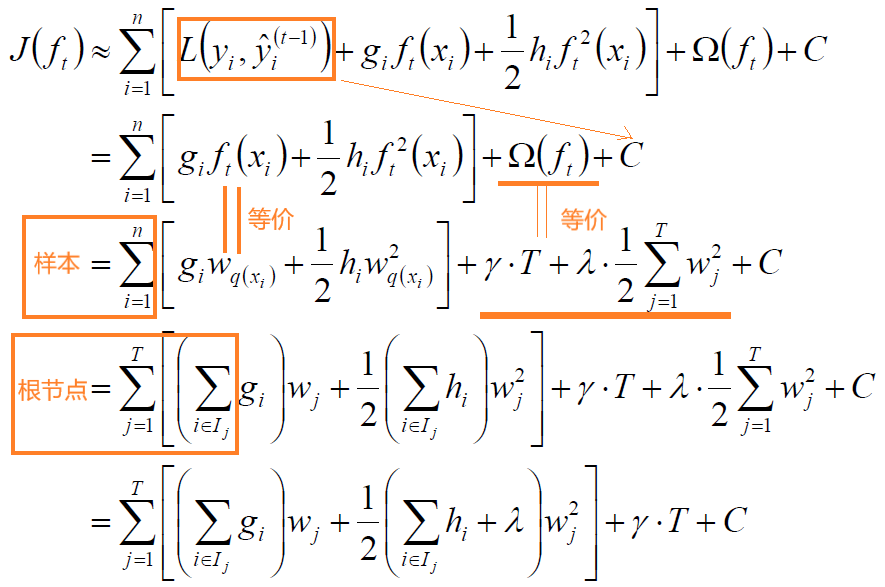
对于

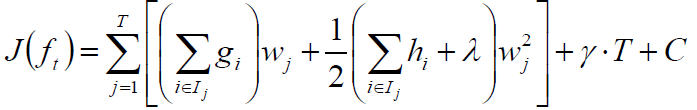
令：

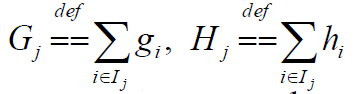
得：

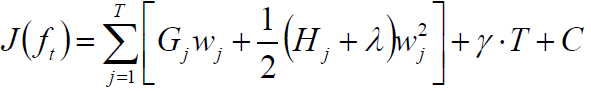
对w求偏导：

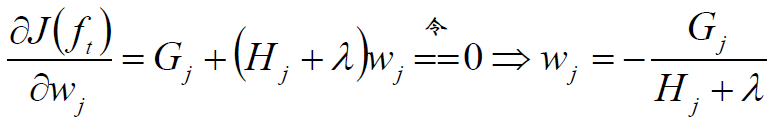
代入上一步的目标函数$J(f_t)$得：

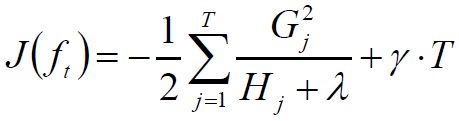
XGBoost中树结构的生成

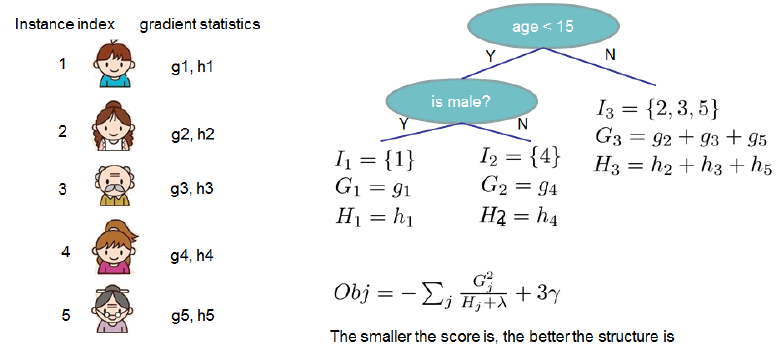
• 构造决策树的结构：枚举可行的分割点，选择增益最大的划分

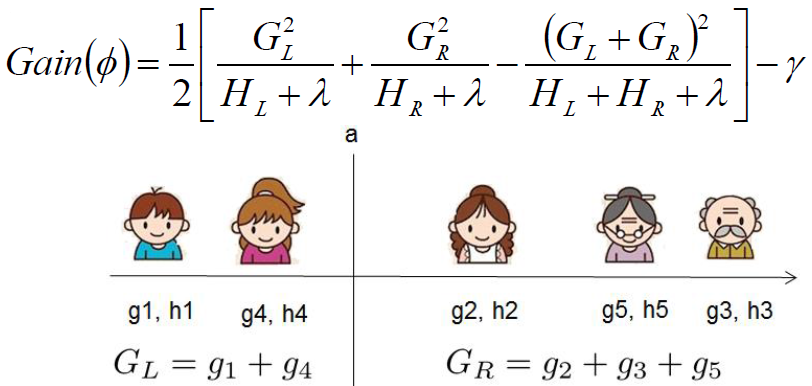
代码1

sklearn并没有集成xgboost，使用前需安装 命令:pip install xgboost

读取数据

XGBoost中数据形式可以是libsvm的，libsvm作用是对稀疏特征进行优化，看个例子：
1 101:1.2 102:0.03
0 1:2.1 10001:300 10002:400
0 2:1.2 1212:21 7777:2
每行表示一个样本，每行开头0，1表示标签，而后面的则是特征索引：数值，其他未表示都是0.

我们以判断蘑菇是否有毒为例子来做后续的训练。数据集来自：http://archive.ics.uci.edu/ml/machine-learning-databases/mushroom/ ，其中蘑菇有22个属性，将这些原始的特征加工后得到126维特征，并保存为libsvm格式，标签是表示蘑菇是否有毒。

import xgboost as xgb
data_train = xgb.DMatrix('data/agaricus.txt.train')
data_test = xgb.DMatrix('data/agaricus.txt.test')

设置参数

• eta：可看成学习率learning_rate。典型值一般设置为：0.01-0.2

• gamma：分裂节点时，损失函数减小值只有大于等于gamma才分裂，gamma值越大，算法越保守，越不容易过拟合，但性能就不一定能保证，需要平衡。

• objective

  • reg:linear：线性回归
  • reg:logistic：逻辑回归
  • binary:logistic 二分类的逻辑回归，返回预测的概率
  • binary:logitraw：二分类逻辑回归，输出是逻辑为0/1的前一步的分数
  • multi:softmax：用于Xgboost 做多分类问题，需要设置num_class（分类的个数）
  • multi:softprob：和softmax一样，但是返回的是每个数据属于各个类别的概率。
  • rank:pairwise：让Xgboost 做排名任务，通过最小化(Learn to rank的一种方法)

• max_depth：决策树最大深度

• silent：0 (silent), 1 (warning), 2 (info), 3 (debug)

  更多参数参见：https://xgboost.readthedocs.io/en/latest/parameter.html

param = {'max_depth': 3, 'eta': 0.3, 'objective': 'binary:logistic'}
watchlist = [(data_test, 'eval'), (data_train, 'train')]
n_round = 6
model = xgb.train(param, data_train, num_boost_round=n_round, evals=watchlist)

计算准确率

y_hat = model.predict(data_test)
y_pred = y_hat.copy()
y_pred[y_hat>=0.5]=1
y_pred[y_hat<0.5]=0
y = data_test.get_label()
from sklearn.metrics import accuracy_score
print('accuracy_score=',accuracy_score(y,y_pred))

输出：

accuracy_score= 1.0

查看[0-5]颗决策树

from matplotlib import pyplot
import graphviz
xgb.to_graphviz(model, num_trees=1) # 以第二颗为例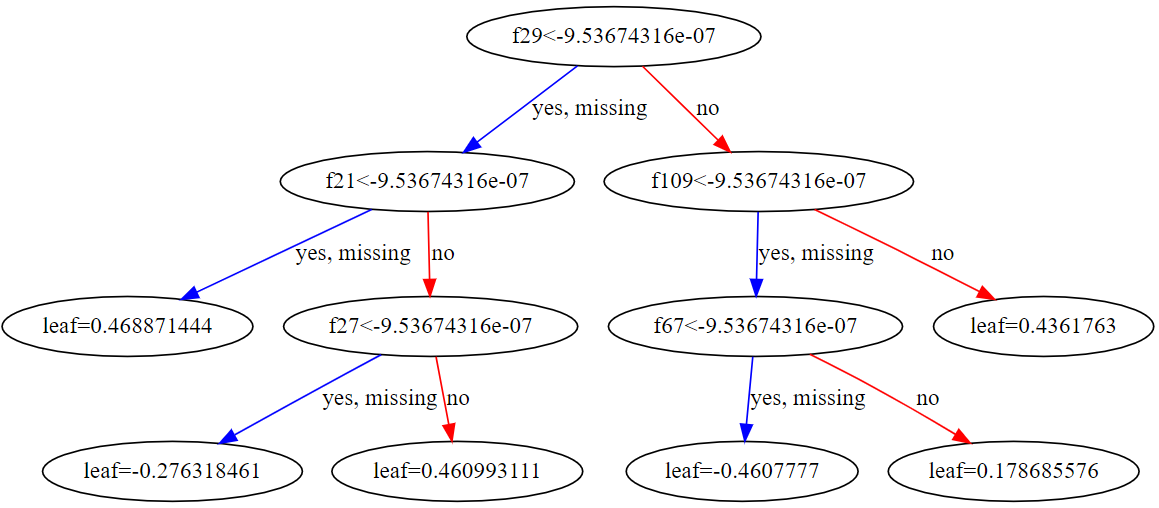

代码2

(写法不同)

import xgboost as xgb
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
# 读取数据(把libsvm格式读取成以前我们常用的二维数组形式)
from sklearn.datasets import load_svmlight_file
#data_train = xgb.DMatrix('data/agaricus.txt.train')
#data_test = xgb.DMatrix('data/agaricus.txt.test')
X_train,y_train = load_svmlight_file('data/agaricus.txt.train')
X_test,y_test = load_svmlight_file('data/agaricus.txt.test')
# 把稀疏数组转换为稠密数组
X_train.toarray().shape
# (6513, 126)
# 设置参数
model =xgb.XGBClassifier(max_depth=2, learning_rate=1, n_estimators=6, objective='binary:logistic')

model.fit(X_train, y_train)
# 计算准确率
# 训练集上准确率
train_preds = model.predict(X_train)
train_predictions = [round(value) for value in train_preds]

train_accuracy = accuracy_score(y_train, train_predictions)
print ("Train Accuary: %.2f%%" % (train_accuracy * 100.0))
# 测试集上准确率
# make prediction
preds = model.predict(X_test)
predictions = [round(value) for value in preds]

test_accuracy = accuracy_score(y_test, predictions)
print("Test Accuracy: %.2f%%" % (test_accuracy * 100.0))

输出：

Train Accuary: 99.88%
Test Accuracy: 100.00%

GridSearchcv搜索最优参数

from sklearn.model_selection import GridSearchCV
model = xgb.XGBClassifier(learning_rate=0.1, objective='binary:logistic')
param_grid = {
 'n_estimators': range(1, 51, 1),
 'max_depth':range(1,10,1)
}
clf = GridSearchCV(model, param_grid, "accuracy",cv=5)
clf.fit(X_train, y_train)
print(clf.best_params_, clf.best_score_)

输出：

({'max_depth': 2, 'n_estimators': 30}, 0.9841860859908541)

early-stop

设置验证valid集，迭代过程中发现在验证集上错误率增加，则提前停止迭代。

from sklearn.model_selection import train_test_split
X_train_part, X_validate, y_train_part, y_validate = train_test_split(X_train, y_train, test_size=0.3,random_state=0)
# 设置boosting迭代计算次数
num_round = 100

bst =xgb.XGBClassifier(max_depth=2, learning_rate=0.1, n_estimators=num_round, objective='binary:logistic')

eval_set =[(X_validate, y_validate)]
# early_stopping_rounds：连续x次在验证集的错误率均不变或上升时即停止。
bst.fit(X_train_part, y_train_part, early_stopping_rounds=10, eval_metric="error", eval_set=eval_set, verbose=True)

输出：

[0]	validation_0-error:0.04862
Will train until validation_0-error hasn't improved in 10 rounds.
[1]	validation_0-error:0.04299
[2]	validation_0-error:0.04862
[3]	validation_0-error:0.04299
[4]	validation_0-error:0.04862
[5]	validation_0-error:0.04862
[6]	validation_0-error:0.04299
[7]	validation_0-error:0.04299
[8]	validation_0-error:0.04299
[9]	validation_0-error:0.04299
[10]	validation_0-error:0.04299
[11]	validation_0-error:0.02405
[12]	validation_0-error:0.02968
[13]	validation_0-error:0.01945
[14]	validation_0-error:0.01945
[15]	validation_0-error:0.01945
[16]	validation_0-error:0.01945
[17]	validation_0-error:0.01945
[18]	validation_0-error:0.01945
[19]	validation_0-error:0.01945
[20]	validation_0-error:0.01945
[21]	validation_0-error:0.02661
[22]	validation_0-error:0.02354
[23]	validation_0-error:0.02354
Stopping. Best iteration:
[13]	validation_0-error:0.01945

Out[13]:

XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
              colsample_bynode=1, colsample_bytree=1, gamma=0, gpu_id=-1,
              importance_type='gain', interaction_constraints='',
              learning_rate=0.1, max_delta_step=0, max_depth=2,
              min_child_weight=1, missing=nan, monotone_constraints='()',
              n_estimators=100, n_jobs=0, num_parallel_tree=1,
              objective='binary:logistic', random_state=0, reg_alpha=0,
              reg_lambda=1, scale_pos_weight=1, subsample=1,
              tree_method='exact', validate_parameters=1, verbosity=None)

将错误率可视化，进行更直观的观察。

results = bst.evals_result()
epochs = len(results['validation_0']['error'])
x_axis = range(0, epochs)

# plot log loss
plt.plot(x_axis, results['validation_0']['error'], label='Test')

plt.ylabel('Error')
plt.xlabel('Round')
plt.title('XGBoost Early Stop')
plt.show()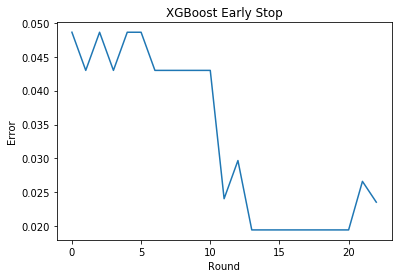

可视化学习曲线

训练

# 设置boosting迭代计算次数
num_round = 100

# 没有 eraly_stop
bst =xgb.XGBClassifier(max_depth=2, learning_rate=0.1, n_estimators=num_round, silent=True, objective='binary:logistic')
 
eval_set = [(X_train_part, y_train_part), (X_validate, y_validate)]
bst.fit(X_train_part, y_train_part, eval_metric=["error", "logloss"], eval_set=eval_set, verbose=True)

输出：

[0]	validation_0-error:0.04562	validation_0-logloss:0.61466	validation_1-error:0.04862	validation_1-logloss:0.61509
[1]	validation_0-error:0.04102	validation_0-logloss:0.55002	validation_1-error:0.04299	validation_1-logloss:0.55021
[2]	validation_0-error:0.04562	validation_0-logloss:0.49553	validation_1-error:0.04862	validation_1-logloss:0.49615
[3]	validation_0-error:0.04102	validation_0-logloss:0.44924	validation_1-error:0.04299	validation_1-logloss:0.44970
[4]	validation_0-error:0.04562	validation_0-logloss:0.40965	validation_1-error:0.04862	validation_1-logloss:0.41051
[5]	validation_0-error:0.04562	validation_0-logloss:0.37502	validation_1-error:0.04862	validation_1-logloss:0.37527
[6]	validation_0-error:0.04102	validation_0-logloss:0.34374	validation_1-error:0.04299	validation_1-logloss:0.34409
[7]	validation_0-error:0.04102	validation_0-logloss:0.31648	validation_1-error:0.04299	validation_1-logloss:0.31680
[8]	validation_0-error:0.04102	validation_0-logloss:0.29229	validation_1-error:0.04299	validation_1-logloss:0.29217
[9]	validation_0-error:0.04102	validation_0-logloss:0.27028	validation_1-error:0.04299	validation_1-logloss:0.27031
[10]	validation_0-error:0.04102	validation_0-logloss:0.25084	validation_1-error:0.04299	validation_1-logloss:0.25075
[11]	validation_0-error:0.02303	validation_0-logloss:0.23349	validation_1-error:0.02405	validation_1-logloss:0.23322
[12]	validation_0-error:0.02895	validation_0-logloss:0.21413	validation_1-error:0.02968	validation_1-logloss:0.21411
[13]	validation_0-error:0.01645	validation_0-logloss:0.19726	validation_1-error:0.01945	validation_1-logloss:0.19747
[14]	validation_0-error:0.01645	validation_0-logloss:0.18254	validation_1-error:0.01945	validation_1-logloss:0.18296
[15]	validation_0-error:0.01645	validation_0-logloss:0.16969	validation_1-error:0.01945	validation_1-logloss:0.17029
[16]	validation_0-error:0.01645	validation_0-logloss:0.15845	validation_1-error:0.01945	validation_1-logloss:0.15923
[17]	validation_0-error:0.01645	validation_0-logloss:0.14999	validation_1-error:0.01945	validation_1-logloss:0.15106
[18]	validation_0-error:0.01645	validation_0-logloss:0.14108	validation_1-error:0.01945	validation_1-logloss:0.14227
[19]	validation_0-error:0.01645	validation_0-logloss:0.13417	validation_1-error:0.01945	validation_1-logloss:0.13544
[20]	validation_0-error:0.01645	validation_0-logloss:0.12691	validation_1-error:0.01945	validation_1-logloss:0.12827
[21]	validation_0-error:0.02500	validation_0-logloss:0.12055	validation_1-error:0.02661	validation_1-logloss:0.12199
[22]	validation_0-error:0.02062	validation_0-logloss:0.11535	validation_1-error:0.02354	validation_1-logloss:0.11683
[23]	validation_0-error:0.02062	validation_0-logloss:0.11015	validation_1-error:0.02354	validation_1-logloss:0.11169
[24]	validation_0-error:0.02062	validation_0-logloss:0.10586	validation_1-error:0.02354	validation_1-logloss:0.10725
[25]	validation_0-error:0.02062	validation_0-logloss:0.10196	validation_1-error:0.02354	validation_1-logloss:0.10337
[26]	validation_0-error:0.02062	validation_0-logloss:0.09799	validation_1-error:0.02354	validation_1-logloss:0.09945
[27]	validation_0-error:0.02062	validation_0-logloss:0.09453	validation_1-error:0.02354	validation_1-logloss:0.09620
[28]	validation_0-error:0.02062	validation_0-logloss:0.09112	validation_1-error:0.02354	validation_1-logloss:0.09283
[29]	validation_0-error:0.02062	validation_0-logloss:0.08809	validation_1-error:0.02354	validation_1-logloss:0.08991
[30]	validation_0-error:0.02062	validation_0-logloss:0.08521	validation_1-error:0.02354	validation_1-logloss:0.08693
[31]	validation_0-error:0.02062	validation_0-logloss:0.08188	validation_1-error:0.02354	validation_1-logloss:0.08324
[32]	validation_0-error:0.02062	validation_0-logloss:0.07883	validation_1-error:0.02354	validation_1-logloss:0.08027
[33]	validation_0-error:0.02062	validation_0-logloss:0.07606	validation_1-error:0.02354	validation_1-logloss:0.07722
[34]	validation_0-error:0.02062	validation_0-logloss:0.07349	validation_1-error:0.02354	validation_1-logloss:0.07491
[35]	validation_0-error:0.02062	validation_0-logloss:0.07078	validation_1-error:0.02354	validation_1-logloss:0.07213
[36]	validation_0-error:0.01470	validation_0-logloss:0.06844	validation_1-error:0.01791	validation_1-logloss:0.06985
[37]	validation_0-error:0.01009	validation_0-logloss:0.06620	validation_1-error:0.01023	validation_1-logloss:0.06742
[38]	validation_0-error:0.01470	validation_0-logloss:0.06400	validation_1-error:0.01791	validation_1-logloss:0.06544
[39]	validation_0-error:0.00153	validation_0-logloss:0.06188	validation_1-error:0.00307	validation_1-logloss:0.06349
[40]	validation_0-error:0.00153	validation_0-logloss:0.05988	validation_1-error:0.00307	validation_1-logloss:0.06132
[41]	validation_0-error:0.00153	validation_0-logloss:0.05798	validation_1-error:0.00307	validation_1-logloss:0.05936
[42]	validation_0-error:0.00153	validation_0-logloss:0.05621	validation_1-error:0.00307	validation_1-logloss:0.05774
[43]	validation_0-error:0.00153	validation_0-logloss:0.05441	validation_1-error:0.00307	validation_1-logloss:0.05600
[44]	validation_0-error:0.00153	validation_0-logloss:0.05274	validation_1-error:0.00307	validation_1-logloss:0.05426
[45]	validation_0-error:0.00153	validation_0-logloss:0.05121	validation_1-error:0.00307	validation_1-logloss:0.05266
[46]	validation_0-error:0.00153	validation_0-logloss:0.04972	validation_1-error:0.00307	validation_1-logloss:0.05131
[47]	validation_0-error:0.00153	validation_0-logloss:0.04820	validation_1-error:0.00307	validation_1-logloss:0.04985
[48]	validation_0-error:0.00153	validation_0-logloss:0.04680	validation_1-error:0.00307	validation_1-logloss:0.04838
[49]	validation_0-error:0.00153	validation_0-logloss:0.04552	validation_1-error:0.00307	validation_1-logloss:0.04715
[50]	validation_0-error:0.00153	validation_0-logloss:0.04423	validation_1-error:0.00307	validation_1-logloss:0.04583
[51]	validation_0-error:0.00153	validation_0-logloss:0.04302	validation_1-error:0.00307	validation_1-logloss:0.04456
[52]	validation_0-error:0.00153	validation_0-logloss:0.04190	validation_1-error:0.00307	validation_1-logloss:0.04358
[53]	validation_0-error:0.00153	validation_0-logloss:0.04072	validation_1-error:0.00307	validation_1-logloss:0.04234
[54]	validation_0-error:0.00153	validation_0-logloss:0.03967	validation_1-error:0.00307	validation_1-logloss:0.04134
[55]	validation_0-error:0.00153	validation_0-logloss:0.03866	validation_1-error:0.00307	validation_1-logloss:0.04027
[56]	validation_0-error:0.00153	validation_0-logloss:0.03766	validation_1-error:0.00307	validation_1-logloss:0.03940
[57]	validation_0-error:0.00153	validation_0-logloss:0.03663	validation_1-error:0.00307	validation_1-logloss:0.03849
[58]	validation_0-error:0.00153	validation_0-logloss:0.03569	validation_1-error:0.00307	validation_1-logloss:0.03751
[59]	validation_0-error:0.00153	validation_0-logloss:0.03482	validation_1-error:0.00307	validation_1-logloss:0.03658
[60]	validation_0-error:0.00153	validation_0-logloss:0.03393	validation_1-error:0.00307	validation_1-logloss:0.03581
[61]	validation_0-error:0.00153	validation_0-logloss:0.03272	validation_1-error:0.00307	validation_1-logloss:0.03450
[62]	validation_0-error:0.00153	validation_0-logloss:0.03192	validation_1-error:0.00307	validation_1-logloss:0.03367
[63]	validation_0-error:0.00153	validation_0-logloss:0.03116	validation_1-error:0.00307	validation_1-logloss:0.03295
[64]	validation_0-error:0.00153	validation_0-logloss:0.03041	validation_1-error:0.00307	validation_1-logloss:0.03216
[65]	validation_0-error:0.00153	validation_0-logloss:0.02968	validation_1-error:0.00307	validation_1-logloss:0.03140
[66]	validation_0-error:0.00153	validation_0-logloss:0.02901	validation_1-error:0.00307	validation_1-logloss:0.03079
[67]	validation_0-error:0.00153	validation_0-logloss:0.02834	validation_1-error:0.00307	validation_1-logloss:0.03017
[68]	validation_0-error:0.00153	validation_0-logloss:0.02771	validation_1-error:0.00307	validation_1-logloss:0.02948
[69]	validation_0-error:0.00153	validation_0-logloss:0.02708	validation_1-error:0.00307	validation_1-logloss:0.02896
[70]	validation_0-error:0.00153	validation_0-logloss:0.02646	validation_1-error:0.00307	validation_1-logloss:0.02834
[71]	validation_0-error:0.00153	validation_0-logloss:0.02589	validation_1-error:0.00307	validation_1-logloss:0.02773
[72]	validation_0-error:0.00153	validation_0-logloss:0.02533	validation_1-error:0.00307	validation_1-logloss:0.02712
[73]	validation_0-error:0.00153	validation_0-logloss:0.02479	validation_1-error:0.00307	validation_1-logloss:0.02663
[74]	validation_0-error:0.00153	validation_0-logloss:0.02427	validation_1-error:0.00307	validation_1-logloss:0.02600
[75]	validation_0-error:0.00153	validation_0-logloss:0.02376	validation_1-error:0.00307	validation_1-logloss:0.02553
[76]	validation_0-error:0.00153	validation_0-logloss:0.02327	validation_1-error:0.00307	validation_1-logloss:0.02512
[77]	validation_0-error:0.00153	validation_0-logloss:0.02278	validation_1-error:0.00307	validation_1-logloss:0.02461
[78]	validation_0-error:0.00153	validation_0-logloss:0.02233	validation_1-error:0.00307	validation_1-logloss:0.02421
[79]	validation_0-error:0.00153	validation_0-logloss:0.02186	validation_1-error:0.00307	validation_1-logloss:0.02378
[80]	validation_0-error:0.00153	validation_0-logloss:0.02143	validation_1-error:0.00307	validation_1-logloss:0.02330
[81]	validation_0-error:0.00153	validation_0-logloss:0.02090	validation_1-error:0.00307	validation_1-logloss:0.02271
[82]	validation_0-error:0.00153	validation_0-logloss:0.02050	validation_1-error:0.00307	validation_1-logloss:0.02239
[83]	validation_0-error:0.00153	validation_0-logloss:0.02009	validation_1-error:0.00307	validation_1-logloss:0.02206
[84]	validation_0-error:0.00153	validation_0-logloss:0.01969	validation_1-error:0.00307	validation_1-logloss:0.02159
[85]	validation_0-error:0.00153	validation_0-logloss:0.01931	validation_1-error:0.00307	validation_1-logloss:0.02126
[86]	validation_0-error:0.00153	validation_0-logloss:0.01895	validation_1-error:0.00307	validation_1-logloss:0.02088
[87]	validation_0-error:0.00153	validation_0-logloss:0.01837	validation_1-error:0.00307	validation_1-logloss:0.02021
[88]	validation_0-error:0.00153	validation_0-logloss:0.01804	validation_1-error:0.00307	validation_1-logloss:0.01992
[89]	validation_0-error:0.00153	validation_0-logloss:0.01772	validation_1-error:0.00307	validation_1-logloss:0.01956
[90]	validation_0-error:0.00153	validation_0-logloss:0.01741	validation_1-error:0.00307	validation_1-logloss:0.01929
[91]	validation_0-error:0.00153	validation_0-logloss:0.01710	validation_1-error:0.00307	validation_1-logloss:0.01897
[92]	validation_0-error:0.00153	validation_0-logloss:0.01660	validation_1-error:0.00307	validation_1-logloss:0.01839
[93]	validation_0-error:0.00153	validation_0-logloss:0.01602	validation_1-error:0.00307	validation_1-logloss:0.01748
[94]	validation_0-error:0.00153	validation_0-logloss:0.01576	validation_1-error:0.00307	validation_1-logloss:0.01721
[95]	validation_0-error:0.00153	validation_0-logloss:0.01547	validation_1-error:0.00307	validation_1-logloss:0.01692
[96]	validation_0-error:0.00153	validation_0-logloss:0.01520	validation_1-error:0.00307	validation_1-logloss:0.01672
[97]	validation_0-error:0.00153	validation_0-logloss:0.01492	validation_1-error:0.00307	validation_1-logloss:0.01640
[98]	validation_0-error:0.00153	validation_0-logloss:0.01444	validation_1-error:0.00307	validation_1-logloss:0.01570
[99]	validation_0-error:0.00153	validation_0-logloss:0.01422	validation_1-error:0.00307	validation_1-logloss:0.01543
XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
              colsample_bynode=1, colsample_bytree=1, gamma=0, gpu_id=-1,
              importance_type='gain', interaction_constraints='',
              learning_rate=0.1, max_delta_step=0, max_depth=2,
              min_child_weight=1, missing=nan, monotone_constraints='()',
              n_estimators=100, n_jobs=0, num_parallel_tree=1,
              objective='binary:logistic', random_state=0, reg_alpha=0,
              reg_lambda=1, scale_pos_weight=1, silent=True, subsample=1,
              tree_method='exact', validate_parameters=1, verbosity=None)

可视化

# retrieve performance metrics
results = bst.evals_result()
#print(results)


epochs = len(results['validation_0']['error'])
x_axis = range(0, epochs)

# plot log loss
fig, ax = plt.subplots()
ax.plot(x_axis, results['validation_0']['logloss'], label='Train')
ax.plot(x_axis, results['validation_1']['logloss'], label='Test')
ax.legend()
plt.ylabel('Log Loss')
plt.title('XGBoost Log Loss')
plt.show()

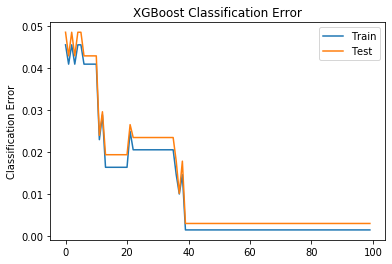
# plot classification error
fig, ax = plt.subplots()
ax.plot(x_axis, results['validation_0']['error'], label='Train')
ax.plot(x_axis, results['validation_1']['error'], label='Test')
ax.legend() # 显示标签label
plt.ylabel('Classification Error')
plt.title('XGBoost Classification Error')
plt.show()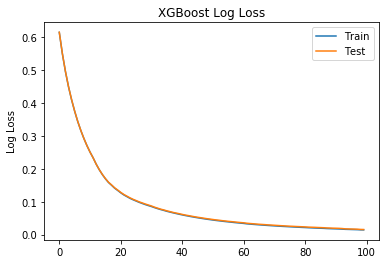

Stacking(堆叠)

Stacking原理

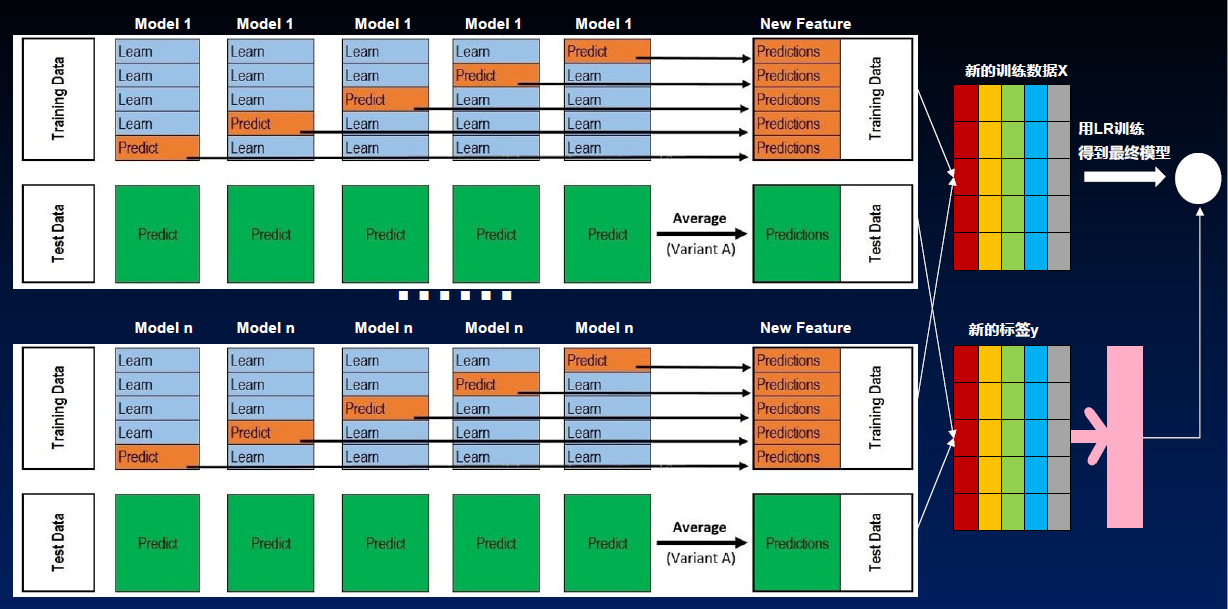
Stacking代码

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import numpy as np
data = np.loadtxt('data/wine.data', delimiter=',')
X = data[:, 1:]
y = data[:, 0:1]
X_train, X_test, y_train, y_test = train_test_split(X, y.ravel(), train_size=0.8, random_state=0)
# 定义基分类器
clf1 = KNeighborsClassifier(n_neighbors=5)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
# 定义最终使用的逻辑回归分类器
lr = LogisticRegression()
# 使用stacking分类器
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3],
                          meta_classifier=lr,use_probas=True)
# 对每一个模型分别进行评价
for model in [clf1,clf2,clf3,lr,sclf]:
    model.fit(X_train,y_train)
    y_test_hat = model.predict(X_test)
    print(model.__class__.__name__,',test accuarcy:',accuracy_score(y_test,y_test_hat))

输出：

KNeighborsClassifier ,test accuarcy: 0.8055555555555556
RandomForestClassifier ,test accuarcy: 0.9444444444444444
GaussianNB ,test accuarcy: 0.9166666666666666
LogisticRegression ,test accuarcy: 0.9444444444444444
StackingClassifier ,test accuarcy: 0.9722222222222222