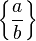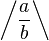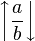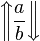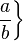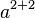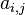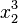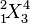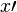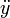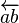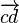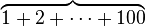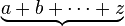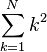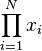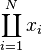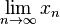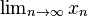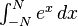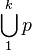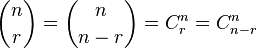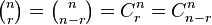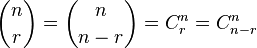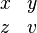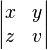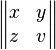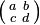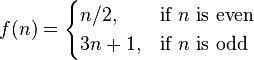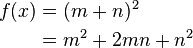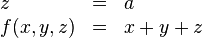Latex常用语法

因为每次都要找，不如总结下来。网页端又显示不正常了，哎，有空闲再调把~

空格

两个quad空格	a \qquad b	$a \qquad b$	两个m的宽度
quad空格	a \quad b	$a \quad b$	一个m的宽度
大空格	a\ b	$a\ b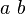$	1/3m宽度
中等空格	a\;b	$a\;b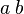$	2/7m宽度
小空格	a\,b	$a\,b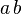$	1/6m宽度
没有空格	ab	$ab\,$
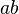紧贴	a!b	$a\!b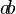$	缩进1/6m*宽度

空格

注意TEX能够自动处理大多数的空格，但是您有时候需要自己来控制。

功能	语法	显示	宽度
2个quad空格	`\alpha\qquad\beta`	$\alpha\qquad\beta$	$2m\$
quad空格	`\alpha\quad\beta`	$\alpha\quad\beta$	$m\$
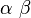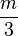大空格	`\alpha\ \beta`	$\alpha\ \beta$	$\frac{m}{3}$
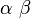中等空格	`\alpha\;\beta`	$\alpha\;\beta$	$\frac{2m}{7}$
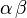小空格	`\alpha\,\beta`	$\alpha\,\beta$	$\frac{m}{6}$
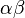没有空格	`\alpha\beta`	$\alpha\beta\$	$0\$
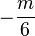紧贴	`\alpha\!\beta`	$\alpha\!\beta$	$-\frac{m}{6}$

声调

语法	效果	语法	效果	语法	效果
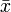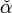\bar{x}	$\bar{x}$	\acute{\eta}	$\acute{\eta}$	\check{\alpha}	$\check{\alpha}$
\grave{\eta}	$\grave{\eta}$	\breve{a}	$\breve{a}$	\ddot{y}	$\ddot{y}$
\dot{x}	$\dot{x}$	\hat{\alpha}	$\hat{\alpha}$	\tilde{\iota}	$\tilde{\iota}$

微分

语法	效果	语法	效果	语法	效果
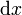\nabla	$\nabla$	\partial x	$\partial x$	\mathrm{d}x	$\mathrm{d}x\$
\dot x	$\dot x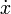$	\ddot y	$\ddot y$

括号

功能	语法	显示
不好看	( \frac{1}{2} )	$( \frac{1}{2} )$
好看了	\left( \frac{1}{2} \right)	$\left ( \frac{1}{2} \right )$

您可以使用 \left 和 \right 来显示不同的括号：

功能	语法	显示
圆括号，小括号	`\left( \frac{a}{b} \right)`	$\left( \frac{a}{b} \right)$
方括号，中括号	`\left[ \frac{a}{b} \right]`	$\left[ \frac{a}{b} \right]$
花括号，大括号	`\left\{ \frac{a}{b} \right\}`	$\left\{ \frac{a}{b} \right\}$
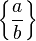角括号	`\left \langle \frac{a}{b} \right \rangle`	$\left\langle \frac{a}{b} \right \rangle$
单竖线，绝对值	`\left\	\frac{a}{b} \right\	`	![\left\	\frac{a}{b} \right\	](http://upload.wikimedia.org/wikipedia/zh/math/4/0/d/40d6c8253b08e8801a01b3f6e5069a62.png)
双竖线，范	`\left \	\frac{a}{b} \right \	`	![\left \	\frac{a}{b} \right \	](http://upload.wikimedia.org/wikipedia/zh/math/f/3/0/f30a5c412d1e4b4e7c6195ff5d47e947.png)
取整函数（Floor function）	`\left \lfloor \frac{a}{b} \right \rfloor`	$\left \lfloor \frac{a}{b} \right \rfloor$
取顶函数（Ceiling function)	`\left \lceil \frac{c}{d} \right \rceil`	$\left \lceil \frac{c}{d} \right \rceil$
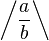斜线与反斜线	`\left / \frac{a}{b} \right \backslash`	$\left / \frac{a}{b} \right \backslash$
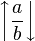上下箭头	`\left \uparrow \frac{a}{b} \right \downarrow`	$\pagecolor{White}\left \uparrow \frac{a}{b} \right \downarrow$
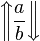上下箭头	`\left \Uparrow \frac{a}{b} \right \Downarrow`	$\pagecolor{White}\left \Uparrow \frac{a}{b} \right \Downarrow$
上下箭头	`\left \updownarrow \frac{a}{b} \right\Updownarrow`	$\pagecolor{White}\left \updownarrow \frac{a}{b} \right \Updownarrow$
混合括号	`\left [ 0,1 \right ) \left \langle \psi \right \	`	$混合括号$ ![\left \langle \psi \right \	](http://upload.wikimedia.org/wikipedia/zh/math/d/a/2/da25fc177fd4c53a2c3399c25685dd4c.png)
单左括号	`\left \{ \frac{a}{b} \right .`	$\left \{ \frac{a}{b} \right .$
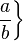单右括号	`\left . \frac{a}{b} \right \}`	$\left . \frac{a}{b} \right \}$

$\left [ 0,1 \right ) \left \langle \psi \right |$

功能	语法	显示
圆括号，小括号	\left( \frac{a}{b} \right)
方括号，中括号	`\left[ \frac{a}{b} \right]`	![\left[ \frac{a}{b} \right]](http://upload.wikimedia.org/wikipedia/zh/math/8/5/8/8585c96f355f7e301fd5143bea32efaf.png)
花括号，大括号	`\left\{ \frac{a}{b} \right\}`	![\left\{ \frac{a}{b} \right\}](http://upload.wikimedia.org/wikipedia/zh/math/c/4/d/c4d4af6bab9a0e6532dddd50e7d27158.png)
角括号	`\left \langle \frac{a}{b} \right \rangle`	![\left\langle \frac{a}{b} \right \rangle](http://upload.wikimedia.org/wikipedia/zh/math/d/0/6/d06e733ce705ed26a7e048dbd2945371.png)
单竖线，绝对值	`\left\\| \frac{a}{b} \right\\|`	![\left\\| \frac{a}{b} \right\\|](http://upload.wikimedia.org/wikipedia/zh/math/4/0/d/40d6c8253b08e8801a01b3f6e5069a62.png)
双竖线，范	`\left \\| \frac{a}{b} \right \\|`	![\left \\| \frac{a}{b} \right \\|](http://upload.wikimedia.org/wikipedia/zh/math/f/3/0/f30a5c412d1e4b4e7c6195ff5d47e947.png)
取整函数（Floor function）	`\left \lfloor \frac{a}{b} \right \rfloor`	![\left \lfloor \frac{a}{b} \right \rfloor](http://upload.wikimedia.org/wikipedia/zh/math/c/0/7/c07e1fc7c0150828e55da4efe37e8a3f.png)
取顶函数（Ceiling function)	`\left \lceil \frac{c}{d} \right \rceil`	![\left \lceil \frac{c}{d} \right \rceil](http://upload.wikimedia.org/wikipedia/zh/math/8/6/8/868c1e52c339e01204aa1a77d44e3c71.png)
斜线与反斜线	`\left / \frac{a}{b} \right \backslash`	![\left / \frac{a}{b} \right \backslash ](http://upload.wikimedia.org/wikipedia/zh/math/2/f/3/2f3c5907c0a4fc4fda69eb71890ce952.png)
<span style='color:blue'>上下箭头</span>	`\left \uparrow \frac{a}{b} \right \downarrow`	![\pagecolor{White}\left \uparrow \frac{a}{b} \right \downarrow ](http://upload.wikimedia.org/wikipedia/zh/math/b/f/8/bf8dd6b753cb6aeb801ea23de51ad5bc.png)
<span style='color:blue'>上下箭头</span>	`\left \Uparrow \frac{a}{b} \right \Downarrow`	![\pagecolor{White}\left \Uparrow \frac{a}{b} \right \Downarrow ](http://upload.wikimedia.org/wikipedia/zh/math/3/d/e/3de7822465115ade10b47634c22b6b7d.png)
<span style='color:blue'>上下箭头</span>	`\left \updownarrow \frac{a}{b} \right\Updownarrow`	![\pagecolor{White}\left \updownarrow \frac{a}{b} \right \Updownarrow](http://upload.wikimedia.org/wikipedia/zh/math/0/6/b/06b15cbba4d935fe84a1a503603e4eb0.png)
混合括号	`\left [ 0,1 \right ) \left \langle \psi \right \\|`	![混合括号](http://upload.wikimedia.org/wikipedia/zh/math/a/3/8/a38771eae1778d0e214f6596a8dc1337.png) ![\left \langle \psi \right \\|](http://upload.wikimedia.org/wikipedia/zh/math/d/a/2/da25fc177fd4c53a2c3399c25685dd4c.png)
单左括号	`\left \{ \frac{a}{b} \right .`	![\left \{ \frac{a}{b} \right .](http://upload.wikimedia.org/wikipedia/zh/math/c/e/d/ced2a2fb558fe49fa56018b9f8fd69d5.png)
单右括号	`\left . \frac{a}{b} \right \}`	![\left . \frac{a}{b} \right \}](http://upload.wikimedia.org/wikipedia/zh/math/9/a/c/9ac9b3c6d21c56f5b2b474b0ea1c4b8a.png)

上标、下标及积分等

功能	语法	效果
上标	`a^2`	$\pagecolor{White} a^2$
下标	`a_2`	$\pagecolor{White} a_2$
组合	`a^{2+2}`	$\pagecolor{White} a^{2+2}$
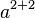组合	`a_{i,j}`	$\pagecolor{White} a_{i,j}$
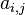结合上下标	`x_2^3`	$\pagecolor{White} x_2^3$
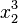前置上下标	`{}_1^2\!X_3^4`	$\pagecolor{White} {}_1^2\!X_3^4$
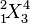导数（HTML）	`x'`	$\pagecolor{White} x'$
导数（PNG）	`x^\prime`	$\pagecolor{White} x^\prime$
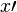导数（错误）	`x\prime`	$\pagecolor{White} x\prime$
导数点	`\dot{x}`	$\pagecolor{White} \dot{x}$
导数点	`\ddot{y}`	$\pagecolor{White} \ddot{y}$
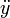向量	`\vec{c}`	$\pagecolor{White} \vec{c}$
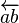向量	`\overleftarrow{a b}`	$\pagecolor{White} \overleftarrow{a b}$
向量	`\overrightarrow{c d}`	$\pagecolor{White} \overrightarrow{c d}$
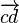向量	`\widehat{e f g}`	$\pagecolor{White} \widehat{e f g}$
上弧	`\overset{\frown} {AB}`	$\pagecolor{White} \overset{\frown} {AB}$
上划线	`\overline{h i j}`	$\pagecolor{White} \overline{h i j}$
下划线	`\underline{k l m}`	$\pagecolor{White} \underline{k l m}$
上括号	`\overbrace{1+2+\cdots+100}`	$\pagecolor{White} \overbrace{1+2+\cdots+100}$
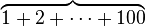上括号	`\begin{matrix} 5050 \\ \overbrace{ 1+2+\cdots+100 }\end{matrix}`	$\pagecolor{White} \begin{matrix} 5050 \\ \overbrace{ 1+2+\cdots+100 } \end{matrix}$
下括号	`\underbrace{a+b+\cdots+z}`	$\pagecolor{White} \underbrace{a+b+\cdots+z}$
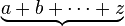下括号	`\begin{matrix} \underbrace{ a+b+\cdots+z } \\ 26\end{matrix}`	$\pagecolor{White} \begin{matrix} \underbrace{ a+b+\cdots+z } \\ 26 \end{matrix}$
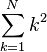求和	`\sum_{k=1}^N k^2`	$\pagecolor{White} \sum_{k=1}^N k^2$
求和	`\begin{matrix} \sum_{k=1}^N k^2 \end{matrix}`	$\pagecolor{White} \begin{matrix} \sum_{k=1}^N k^2 \end{matrix}$
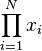求积	`\prod_{i=1}^N x_i`	$\pagecolor{White} \prod_{i=1}^N x_i$
求积	`\begin{matrix} \prod_{i=1}^N x_i \end{matrix}`	$\pagecolor{White} \begin{matrix} \prod_{i=1}^N x_i \end{matrix}$
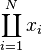上积	`\coprod_{i=1}^N x_i`	$\pagecolor{White} \coprod_{i=1}^N x_i$
上积	`\begin{matrix} \coprod_{i=1}^N x_i\end{matrix}`	$\pagecolor{White} \begin{matrix} \coprod_{i=1}^N x_i \end{matrix}$
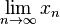极限	`\lim_{n \to \infty}x_n`	$\pagecolor{White} \lim_{n \to \infty}x_n$
极限	`\begin{matrix} \lim_{n \to \infty}x_n\end{matrix}`	$\pagecolor{White} \begin{matrix} \lim_{n \to \infty}x_n \end{matrix}$
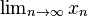积分	`\int_{-N}^{N} e^x\, dx`	$\pagecolor{White} \int_{-N}^{N} e^x\, dx$
积分	`\begin{matrix} \int_{-N}^{N} e^x\, dx\end{matrix}`	$\pagecolor{White} \begin{matrix} \int_{-N}^{N} e^x\, dx \end{matrix}$
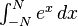双重积分	`\iint_{D}^{W} \, dx\,dy`	$\pagecolor{White} \iint_{D}^{W} \, dx\,dy$
三重积分	`\iiint_{E}^{V} \, dx\,dy\,dz`	$\pagecolor{White} \iiint_{E}^{V} \, dx\,dy\,dz$
四重积分	`\iiiint_{F}^{U} \, dx\,dy\,dz\,dt`	$\pagecolor{White} \iiiint_{F}^{U} \, dx\,dy\,dz\,dt$
闭合的曲线、曲面积分	`\oint_{C} x^3\, dx + 4y^2\, dy`	$\pagecolor{White} \oint_{C} x^3\, dx + 4y^2\, dy$
交集	`\bigcap_1^{n} p`	$\pagecolor{White} \bigcap_1^{n} p$
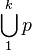并集	`\bigcup_1^{k} p`	$\pagecolor{White} \bigcup_1^{k} p$

上弧 (注: 正确应该用 \overarc, 但在这里行不通。要用建议的语法作为解决办法)

分数、矩阵和多行列式

功能	语法	效果
分数	`\frac{2}{4}=0.5`	$\frac{2}{4}=0.5$
小型分数	`\tfrac{2}{4} = 0.5`	$\tfrac{2}{4} = 0.5$
大型分数（嵌套）	`\cfrac{2}{c + \cfrac{2}{d + \cfrac{2}{4}}} =a`	$\cfrac{2}{c + \cfrac{2}{d + \cfrac{2}{4}}} = a$
大型分数（不嵌套）	`\dfrac{2}{4} = 0.5 \qquad \dfrac{2}{c + \dfrac{2}{d +\dfrac{2}{4}}} = a`	$\dfrac{2}{4} = 0.5 \qquad \dfrac{2}{c + \dfrac{2}{d + \dfrac{2}{4}}} = a$
二项式系数	`\dbinom{n}{r}=\binom{n}{n-r}=C^n_r=C^n_{n-r}`	$\dbinom{n}{r}=\binom{n}{n-r}=C^n_r=C^n_{n-r}$
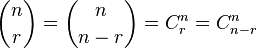小型二项式系数	`\tbinom{n}{r}=\tbinom{n}{n-r}=C^n_r=C^n_{n-r}`	$\tbinom{n}{r}=\tbinom{n}{n-r}=C^n_r=C^n_{n-r}$
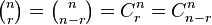大型二项式系数	`\binom{n}{r}=\dbinom{n}{n-r}=C^n_r=C^n_{n-r}`	$\binom{n}{r}=\dbinom{n}{n-r}=C^n_r=C^n_{n-r}$
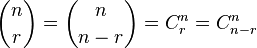矩阵	`\begin{matrix} x & y \\ z & v \end{matrix}`	$\begin{matrix} x & y \\ z & v \end{matrix}$
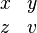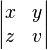矩阵	`\begin{vmatrix} x & y \\ z & v \end{vmatrix}`	$\begin{vmatrix} x & y \\ z & v \end{vmatrix}$
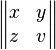矩阵	`\begin{Vmatrix} x & y \\ z & v \end{Vmatrix}`	$\begin{Vmatrix} x & y \\ z & v \end{Vmatrix}$
矩阵	`\begin{bmatrix} 0 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 0 \end{bmatrix}`	$\begin{bmatrix} 0 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 0\end{bmatrix}$
矩阵	`\begin{Bmatrix} x & y \\ z & v \end{Bmatrix}`	$\begin{Bmatrix} x & y \\ z & v \end{Bmatrix}$
矩阵	`\begin{pmatrix} x & y \\ z & v \end{pmatrix}`	$\begin{pmatrix} x & y \\ z & v \end{pmatrix}$
矩阵	`\bigl( \begin{smallmatrix} a&b\\ c&d \end{smallmatrix} \bigr)`	$\bigl( \begin{smallmatrix} a&b\\ c&d \end{smallmatrix} \bigr)$
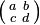条件定义	`f(n) = \begin{cases} n/2, & \mbox{if }n\mbox{ is even} \\ 3n+1, & \mbox{if }n\mbox{ is odd} \end{cases}`	$f(n) = \begin{cases} n/2, & \mbox{if }n\mbox{ is even} \ 3n+1, & \mbox{if }n\mbox{ is odd} \end{cases}$
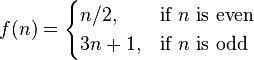多行等式	`\begin{align} f(x) & = (m+n)^2 \\ & = m^2+2mn+n^2 \\ \end{align}`	$\begin{align} f(x) & = (m+n)^2 \ & = m^2+2mn+n^2 \ \end{align}$
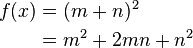多行等式	`\begin{alignat}{2} f(x) & = (m-n)^2 \\ f(x) & = (-m+n)^2 \\ & = m^2-2mn+n^2 \\ \end{alignat}`	$\begin{alignat}{2} f(x) & = (m-n)^2 \ f(x) & = (-m+n)^2 \ & = m^2-2mn+n^2 \ \end{alignat}$
多行等式（左对齐）	`\begin{array}{lcl} z & = & a \\ f(x,y,z) & = & x + y + z \end{array}`	$\begin{array}{lcl} z & = & a \ f(x,y,z) & = & x + y + z \end{array}$
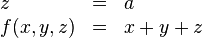多行等式（右对齐）	`\begin{array}{lcr} z & = & a \\ f(x,y,z) & = & x + y + z \end{array}`	$\begin{array}{lcr} z & = & a \ f(x,y,z) & = & x + y + z \end{array}$
长公式换行	`<math>f(x) \,\!</math> <math>= \sum_{n=0}^\infty a_n x^n </math> <math>= a_0+a_1x+a_2x^2+\cdots</math>`	$f(x) \,\!$ $= \sum_{n=0}^\infty a_n x^n$ $= a_0 +a_1x+a_2x^2+\cdots$
方程组	`\begin{cases} 3x + 5y + z \\ 7x - 2y + 4z \\ -6x + 3y + 2z \end{cases}`	$\begin{cases} 3x + 5y + z \\ 7x - 2y + 4z \\ -6x + 3y + 2z \end{cases}$
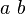
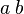
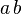
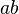
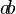
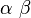
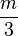
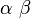
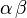
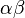
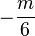
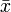
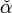
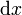
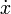
数组	`\begin{array}{	c	c	c	} a & b & S \\ \hline 0&0&1\\ 0&1&1\\ 1&0&1\\ 1&1&0\\ \end{array} `	![ \begin{array}{\	c\	c\	\	c\	} a & b & S \ \hline 0&0&1\ 0&1&1\ 1&0&1\ 1&1&0\ \end{array} ](http://upload.wikimedia.org/wikipedia/zh/math/9/1/5/9151e94ef2bb52c18176dbe4c11921ed.png)