实现power(x,n)，即计算x的n次幂函数。

示例1：

输入: 2.00000, 10
输出: 1024.00000

示例2：

输入: 2.10000, 3
输出: 9.26100

示例3：

输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25

说明：

• -100.0 < x < 100.0
• $n$是32位有符号整数，其数值范围是$[-2^{31},2^{31}-1]$。

快速幂算法：递归和迭代两个版本。
当指数$n$为负数时，可以通过计算$x^{-n}$取倒数得到结果，因此只需要考虑$n$为自然数的情况。

方法一：快速幂+递归(从右到左)

快速幂算法的本质是分治算法。
例子：

$$x \rightarrow x^2 \rightarrow x^4 \rightarrow x^8 \rightarrow x^{16} \rightarrow x^{32} \rightarrow x^{64}$$ $$x \rightarrow x^2 \rightarrow x^4 \rightarrow x^9 \rightarrow x^{19} \rightarrow x^{38} \rightarrow x^{77}$$

第一个直接把上一次的结果平方，第二个把上一个结果平方后，额外乘一个$x$。

• 计算$x^n$时，递归计算出$y=x^{\lfloor n/2 \rfloor}$

• 根据递归计算的结果，如果$n$为偶数，那么$x^n=y^2$；如果$n$为奇数，那么$x^n=y^2*x$；

• 递归的边界为$n=0$，任意数的0次方均为1。

由于每次递归都会使得指数减少一半，因此递归的层数为$O(logn)$，算法可以在很快的时间内得到结果。

复杂度分析：

• 时间复杂度：$O(logn)$，即为递归的层数。
• 空间复杂度：$O(logn)$，即为递归的层数，这是由于递归的函数调用会使用栈空间。

上代码，目前只会python（猛男落泪，等以后会了别的再加上）：

class Solution:
    def myPow(self, x, n):
        def quickMul(N):
            if N == 0:
                return 1.0
            y = quickMul(N // 2)
            return y * y if N % 2 == 0 else y * y * x
        return quickMul(n) if n > 0 else 1.0 / quickMul(-n)

方法二：快速幂 + 迭代(从左到右)

递归需要使用额外的栈空间。递归->迭代。
如果整数$n$的二进制拆分为 $n = 2^{i_0} + 2^{i_1} + \ldots + 2^{i_k}$
借助整数的二进制拆分，得到迭代计算的方法，一般地，如果整数$n$的二进制拆分为：

$$n = 2^{i_0} + 2^{i_1} + \ldots + 2^{i_k}$$

那么

$$x^n = x^{2^{i_0}} * x^{2^{i_1}} * \ldots * x^{2^{i_k}}$$

从$x$不断地进行平方，得到$x^2,x^4,x^8,x^{16},\ldots,$如果$n$的第$k$个（从右往左，从0开始计数）二进制位为1，那么我们就将对应的贡献$x^{2^k}$计入答案。
上代码：

class Solution:
    def myPow(self, x, n):
        def quickMul(N):
            ans = 1.0
            # 贡献的初始值为x
            x_contribute = x
            # 在对N进行二进制拆分的同时计算答案
            while N > 0:
                if N % 2 == 1:
                    # 如果N二进制表示的最低位为1，那么需要计入贡献
                    ans *= x_contribute
                # 将贡献不断地平方
                x_contribute *= x_contribute
                # 舍弃N二进制表示的最低位，这样每次只要判断最低位即可
                N // = 2
            return ans
        return quickMul(n) if n >= 0 else 1.0 / quickMul(-n)

牛顿迭代法

思路参考链接牛顿迭代法快速寻找平方根
代码参考链接leetcode sqrt(x):牛顿迭代法和Quake-III中的神奇方法

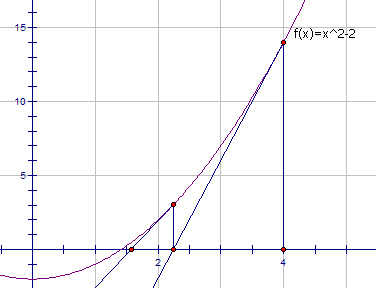
具体求解：牛顿迭代法求解
看了思路，数学真是一个全新的角度~

参考资料

优秀题解(推荐)看了这个大佬的几个题解了，高手，思路很清晰，个人账号里面有一系列套题，剑指Offer之类的，非常具有参考价值。

第一次写，不是很流畅，思路和手都不太行。下周再做一遍，做完就把这行删掉，冲鸭
如此一来，每天水一篇，居然成为了日更博主，哈哈哈哈哈
不足的博文在后期有时间都会进行修改，做一个有质量(没人气)的博主，奥里给O(∩_∩)O。