leetcode 78.子集

给定一组不含重复元素的整数数组nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
示例：

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]
全排列/组合/子集问题，比较相似，可以使用一些通用策略解决。
首先，解空间非常大：

全排列：$N!$
组合：$N!$
子集：$2^N$，每个元素都可能存在或不存在。

在它们的指数级解法中，要确保生成的结果完整且 无冗余，有三种常用的方法：

递归
回溯
基于二进制位掩码和对应位掩码之间的映射字典生成排列/组合/子集

相比前两种方法，第三种方法将每种情况都简化为二进制数，易于实现和验证。
此外，第三种方法具有最优的时间复杂度，可以生成按照字典顺序的输出结果。

方法一：递归

思路
开始假设输出子集为空，每一步都向子集添加新的整数，并生成新的子集。

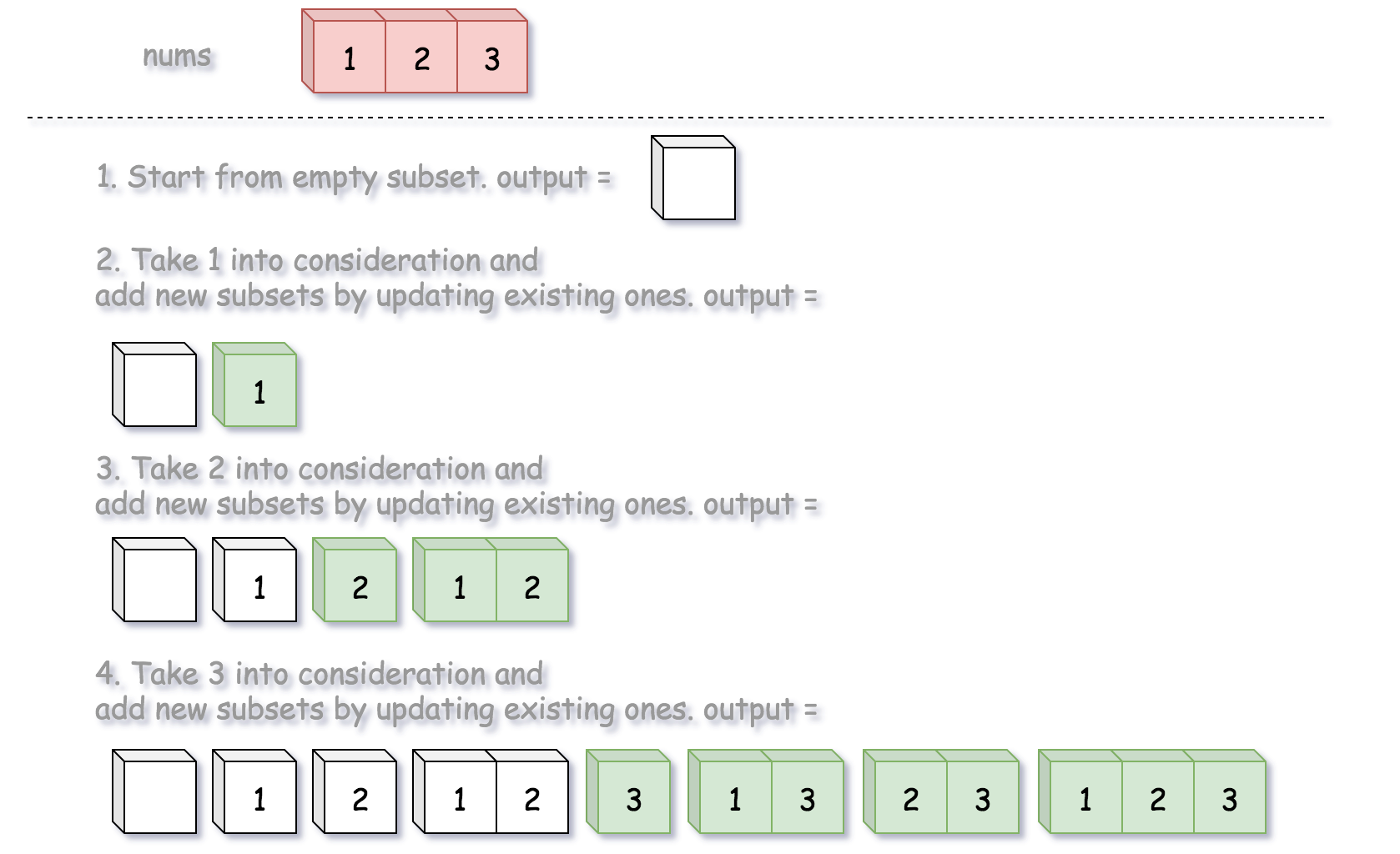
class Solution:
	def subsets(self, nums):
	n = len(nums)
	output = [[]]
	
	for num in nums:
		output += [curr + [num] for curr in output]
	return output

复杂度分析

时间复杂度：$O(N \times 2^N)$，生成所有子集，并复制到输出结果中。???
空间复杂度：$O(N \times 2^N)$，这是子集的数量。???
- 对于给定的任意元素，它在子集中有两种情况，存在或者不存在（对应二进制中的 0 和 1）。因此，N 个数字共有$2^N$个子集。

方法二：回溯

算法

幂集是所有长度从0到n所有子集的组合。

根据定义，该问题可以看作是从序列中生成幂集。
遍历子集长度，通过回溯生成所有给定长度的子集。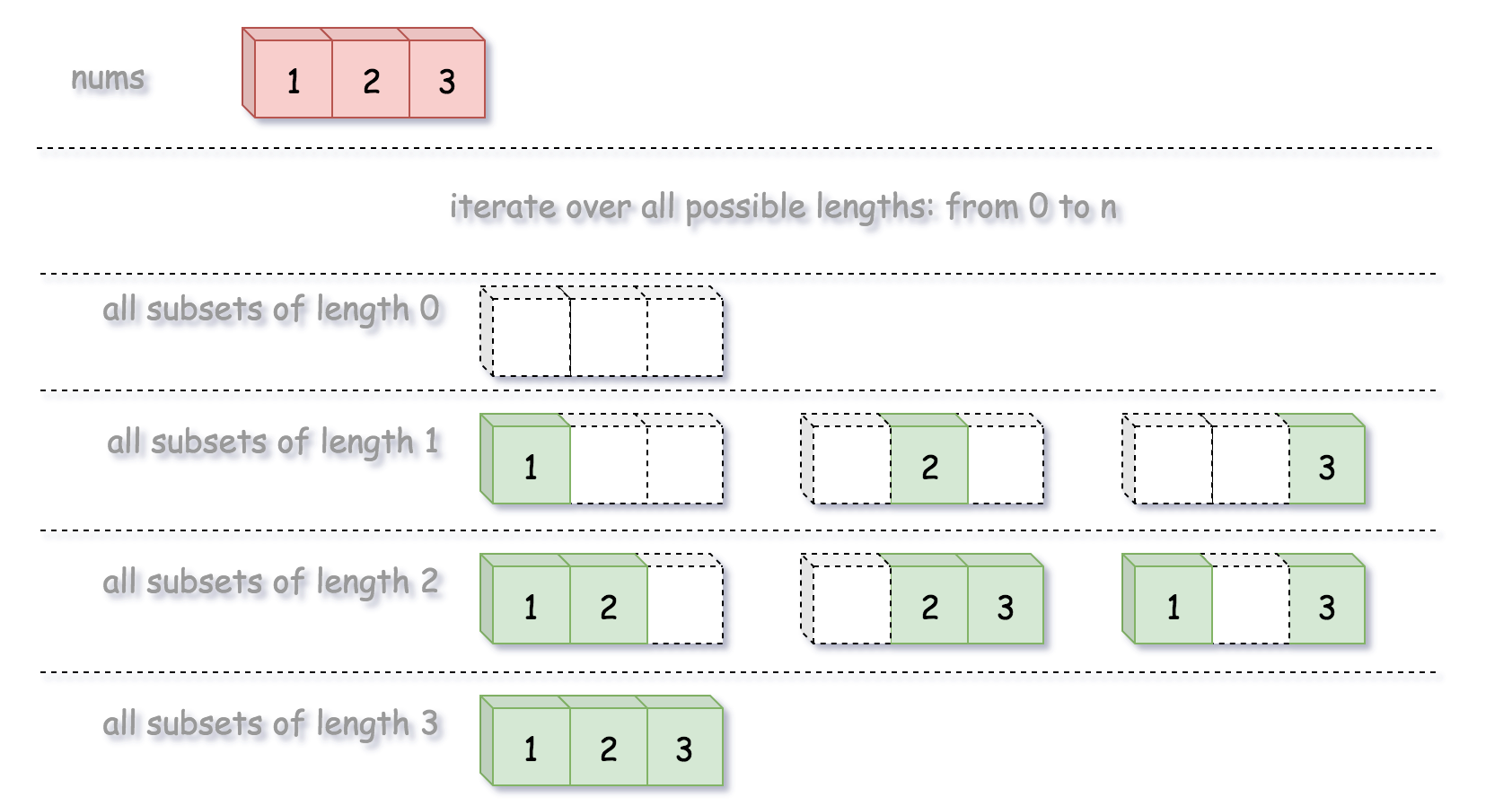

回溯法是一种探索所有潜在可能性找到解决方案的算法。如果当前方案不是正确的解决方案，或者不是最后一个正确的解决方案，则回溯法通过修改上一步的值，则回溯法通过修改上一步的值继续寻找解决方案。

算法
定义一个回溯方法backtrack(first, curr)，第一个参数为索引 first，第二个参数为当前子集 curr。

如果当前子集构造完成，将它添加到输出集合中。
否则，从 first 到 n 遍历索引 i。
- 将整数 nums[i] 添加到当前子集 curr。
- 继续向子集中添加整数：backtrack(i + 1, curr)
- 从 curr 中删除 nums[i] 进行回溯。

class Solution:
    def subsets(self, nums: List[int] -> List[List[int]]):
        def backtrack(first = 0, curr = []):
            # if the combination is done
            if len(curr) == k:
                output.append(curr[:])
            for i in range(first, n):
                # add nums[i] into the current combination
                curr.append(nums[i])
                # use next integers to complete the combination
                backtrack(i+1, curr)
                # backtrack
                curr.pop()
		
        output = []
        n = len(nums)
        for k in range(n + 1):
            backtrack()
       	return output

这里改进了一下，找到了就直接返回上一级。

复杂度分析

时间复杂度：$O(N \times 2^N)$，生成所有子集，并复制到输出集合中。
空间复杂度：$O(N \times 2^N)$，存储所有子集，共n个元素，每个元素都有可能存在或者不存在。

晚上又看到了一种回溯算法：

简化了上面的写法，不用k，也是bfs类似思想，每层的结果都放入output中。但是leetcode的运行时间变长了。(#`O′)

class Solution:
    def subsets(self, nums):
        res = []
        n = len(nums)
        def backtrack(i, tmp):
            res.append(tmp)
            for j in range(i, n):
                backtrack(j+1, tmp + [num[j]])
       	backtrack(0, [])
        return res

append操作是在原List上的修改，不会返回一个新的值。
+运算是对于两个类型相同的变量之间的运算，不改变原有的变量，并返回一个新的值，是内容之间的拼接。
extend 也是在原有List上进行修改，没有返回值，可以扩展不同类型的变量，并将其内容以List变量的形式加入到原List中。
例子：从输出中可见如果extend的是字符串，则字符串会被拆分成字符数组，如果extend的是字典，则字典的key会被加入到List中。

所以这里的tmp+[]不能用tmp.append()替换！哎，猛男落泪，我验证了半天。

本题中回溯类似于bfs，当然用dfs也是可以做的。

方法三：字典排序（二进制排序）子集

思路

该方法思路来自于Donald E. Knuth。

将每个子集映射到长度为 n 的位掩码中，其中第 i 位掩码 nums[i] 为 1，表示第 i 个元素在子集中；如果第 i 位掩码 nums[i] 为 0，表示第 i 个元素不在子集中。

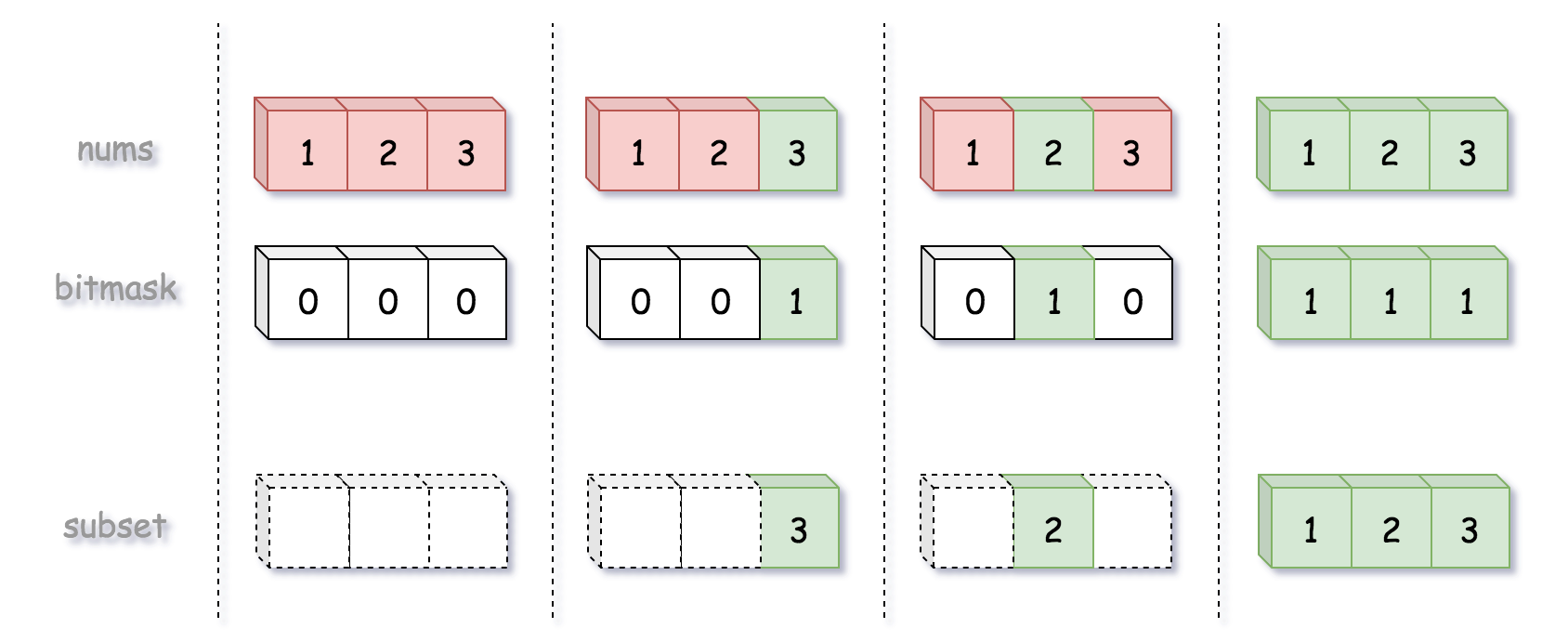
例如，位掩码 0..00（全 0）表示空子集，位掩码 1..11（全 1）表示输入数组 nums。

因此要生成所有子集，只需要生成从 0..00 到 1..11 的所有 n 位掩码。

生成二进制数很简单，但如何处理左边填充 0 是一个问题。因为必须生成固定长度的位掩码：例如 001，而不是 1。因此可以使用一些位操作技巧：

nth_bit = 1 << n
for i in range(2**n):
    # generate bitmask, from 0..00 to 1..11
    bitmask = bin(i | nth_bit)[3:]

以示例为例，就是把[0,7]跟8进行或操作，目的是为了取到前面的0，然后取0b1xxx后三位。

for i in range(2**n, 2**(n + 1)):
    # generate bitmask, from 0..00 to 1..11
    bitmask = bin(i)[3:]

或者直接从8到16，取后三位，效果是一样的。
算法

生成所有长度为 n 的二进制位掩码。
将每个子集都映射到一个位掩码数：位掩码中第 i 位如果是 1 表示子集中存在 nums[i]，0 表示子集中不存在 nums[i]。
返回子集列表。

class Solution:
    def subsets(self, nums):
        n = len(nums)
        output = []
        n_bit = 1 << n
        for i in range(2**n):
            # generate bitmask form 0..00 to 1..11
            bitmask = bin(i|n_bit)[3:]
            # append subset corresponding to that bitmask
            output.append([num[j] for j in range(n) if bitmask[n] == '1'])
   		return output

结束！嗯~ o(￣▽￣)o，收回昨天的话，不难，就是第一次碰到是需要花时间理解，然后就是动手很重要。今日打卡get~

参考资料

leetcode50官方解析

以前觉得只写代码就好了，注释真是太麻烦了。现在的我，只写代码就是耍流氓，要让人理解理解，可读性很很很很重要。