116. 填充每个节点的下一个右侧节点指针

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
	int val;
	Node *left;
	Node *right;
	Node *next;
}

填充它的每个next指针，让这个指针指向下一个右侧节点，如果找不到下一个右侧节点，则将next指针设置为NULL。

初始状态下，所有next指针都被设置为NULL。

示例：

输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":{"$id":"6","left":null,"next":null,"right":null,"val":6},"next":null,"right":{"$id":"7","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":{"$id":"6","left":null,"next":null,"right":null,"val":7},"right":null,"val":6},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"7","left":{"$ref":"5"},"next":null,"right":{"$ref":"6"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"7"},"val":1}

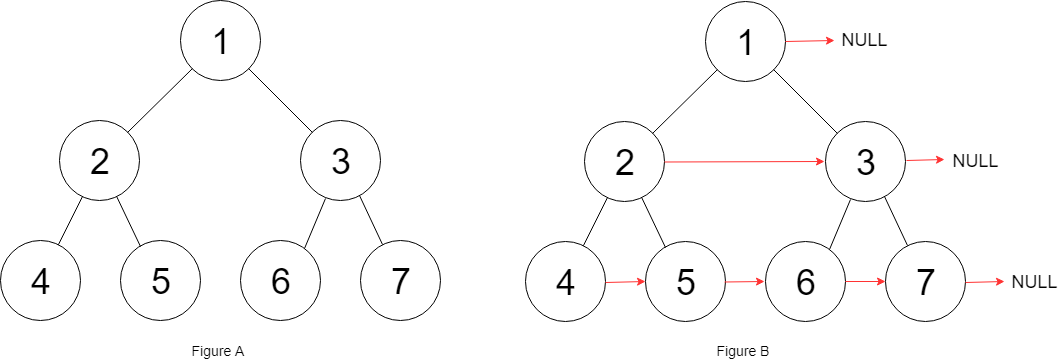
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

思路与算法

方法一：层次遍历

题目要求: 将二叉树的每一层节点都连接起来形成一个链表。
直观做法：对二叉树进行层次遍历，遍历过程中，遍历并连接二叉树每一层节点。

层次遍历：每次将队列中的所有元素进行拓展。保证每次从队列中拿出来遍历的元素属于同一层。遍历过程中修改每个节点的next指针，并拓展下一层的新队列。

广度优先搜素：每次只取出一个节点拓展。

代码：

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return root
        
        Q = collections.deque([root])

        while Q:
            size = len(Q)
            for i in range(size):
                curr = Q.popleft()
                if i == size - 1:
                    pass
                else:
                    curr.next = Q[0]
                if curr.left:
                    Q.append(curr.left)
                if curr.right:
                    Q.append(curr.right)
        return root

复杂度分析：

时间复杂度：$O(N)$。每个节点都被访问一次且只会被访问一次。即从队列中弹出并建立next指针。
空间复杂度：$O(N)$。完美二叉树的最后一个层级包含N/2个节点。广度优先遍历的复杂度取决与一个层级上的最大元素数量。这种情况下空间复杂度为$O(N)$。

方法二：使用已建立的next指针

一颗树中，存在两种类型的next指针。

第一种情况是连接同一个父节点的两个子节点。通过同一个节点直接访问。执行以下操作即可完成连接。
```
node.left.next = node.right
```
第二种情况在不同父亲的子节点之间建立连接，这种情况下无法直接连接。
如果每个节点有指向父节点的指针，可以通过该指针找到next节点。如果不存在该指针，则按照以下思路建立连接：

第N层节点之间建立next指针后，建立第N+1层节点的next指针时，可以通过next指针访问同一层的所有节点。因此可以使用第N层的next指针，为第N+1层节点建立next指针。

node.right.next = node.next.left

完成当前层的连接后，进入下一层重复操作，直到所有的节点全部连接。进入下一层时，需要更新最左节点，然后从新的最左节点开始遍历该层的所有节点。在完美二叉树的设定下，最左节点一定是当前层最左节点的左孩子。如果当前最左节点的左孩子不存在，说明已经达到该树的最后一层，完成了所有节点的连接。

代码：

class Solution:
    def connect(self, root):
        if not root:
            return root
        # 从根节点开始
        leftmost = root
        while leftmost.left:
            # 遍历这一层节点组织成的链表，为下一层的节点更新next指针
            head = leftmost
            while head:
                # connection 1
                head.left.next = head.right
                
                # connection 2
                if head.next:
                    head.right.next = head.next.left
                
                # 指针后移
                head = head.next
            # 去下一层的最左节点
            leftmost = leftmost.left
        return root

复杂度分析：

时间复杂度：$O(N)$，每个节点只访问一次。
空间复杂度：$O(1)$，不需要存储额外的节点。