遍历搜索

在树（图/状态集）中寻找特定结点(Node)

Node节点示例代码

Python

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left, self.right = None, None

C++

struct TreeNode{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x): val(x), left(NULL),right(NULL){}
}

Java

public class TreeNode{
    public int val;
    public TreeNode left, right;
    public TreeNode(int val){
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

搜索-遍历

• 每个节点都要访问一次
• 每个节点仅仅要访问一次
• 对于节点访问顺序不限
  • 深度优先：depth first search
  • 广度优先：breadth first search

示例代码

def dfs(node):
	if node in visited:
        # already visited
        return
    visited.add(node)
    
    # process current node
    # ... # logic here
    dfs(node.left)
    dfs(node.right)

深度优先搜索(Depth-First-Search)

遍历顺序

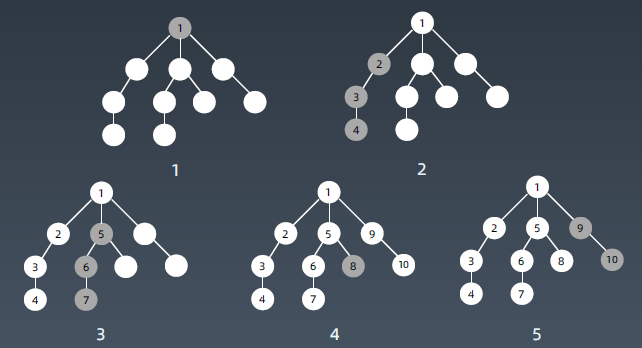
DFS代码-递归写法

visited = set()
def dfs(node, visited):
    if node in visited: # terminator
        # already visited
        return
    
    visited.add(node)
    
    # process current node here.
    ...
    for next_node in node.children():
        if not next_node in visited:
            dfs(next_node, visited)

DFS代码-非递归写法

def DFS(self, tree):
    if tree.root is None:
        return []
    
    visited, stack = [], [tree.root]
    
    while stack:
        node = stack.pop()
        visited.add(node)
        
        process(node)
        nodes = generate_related_nodes(node)
        stack.push(nodes)
    # other processing work
    ...

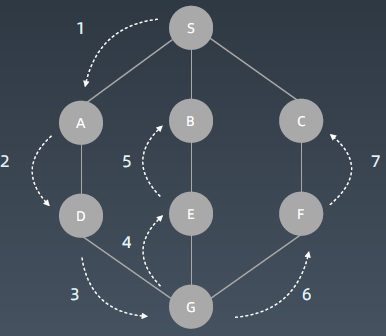
栈：[根节点]->[子节点1，子节点2]->[子节点1，子节点21，子节点22]

广度优先搜索(Breadth-First-Search)

遍历顺序

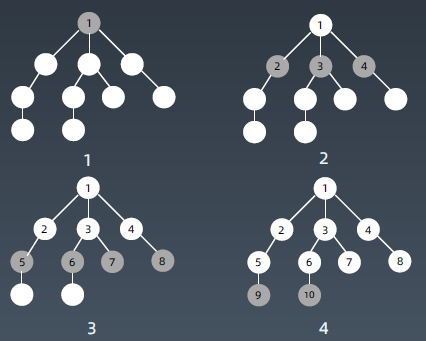
DFS和BFS遍历对比

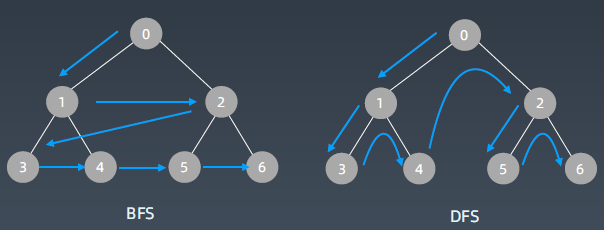
BFS代码

def BFS(graph, start, end):
	queue = []
    queue.append([start])
    visited.add(start)
    
    while queue:
        node = queue.pop()
        visited.add(node)
        
        process(node)
        nodes = generate_related_nodes(node)
        queue.push(nodes)
        
    #other processing work
    ...

递归遍历代码比非递归代码简洁。这是因为递归的方式隐含地使用了系统的 栈，所以此时我们不需要自己维护一个数据结构。