102.二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：
二叉树：[3,9,20,null,null,15,7],

  3
 / \
9  20
  /  \
 15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

方法一：广度优先搜索

思路

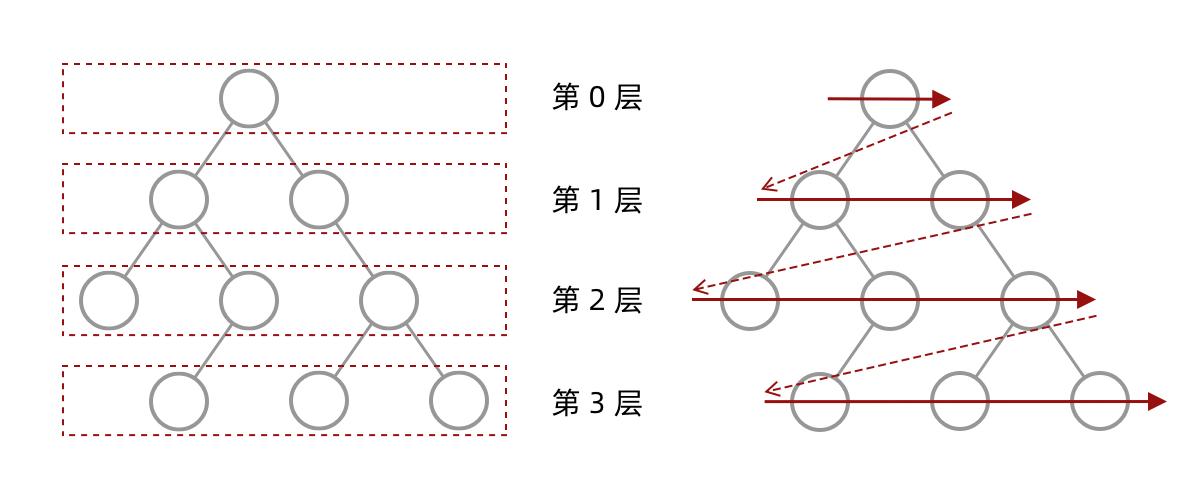
层序遍历就是把二叉树分层，然后每一层从左到右遍历：

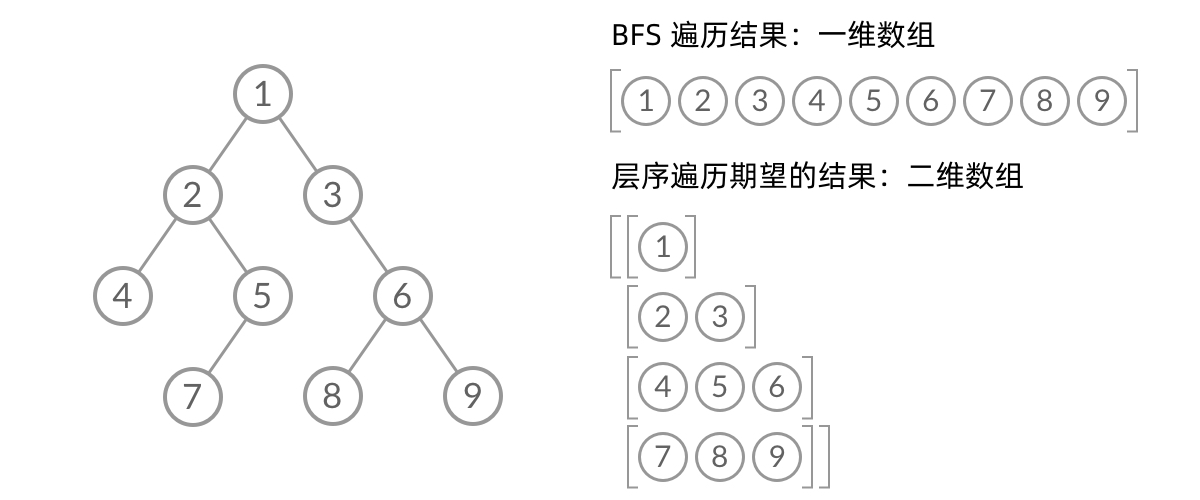
层序遍历要求的输出结果和BFS是不同的。层序遍历要求我们区分每一层，也就是返回二维数组。BFS遍历结果是一个一维数组，无法区分每一层。

如何给BFS遍历结果分层？首先观察BFS遍历过程，结合进队列和出队列的过程：

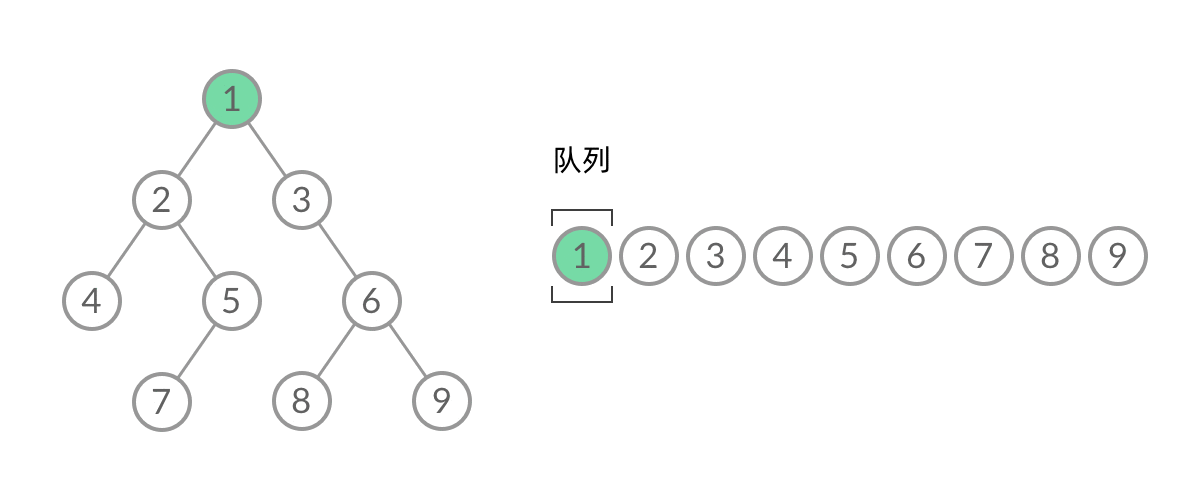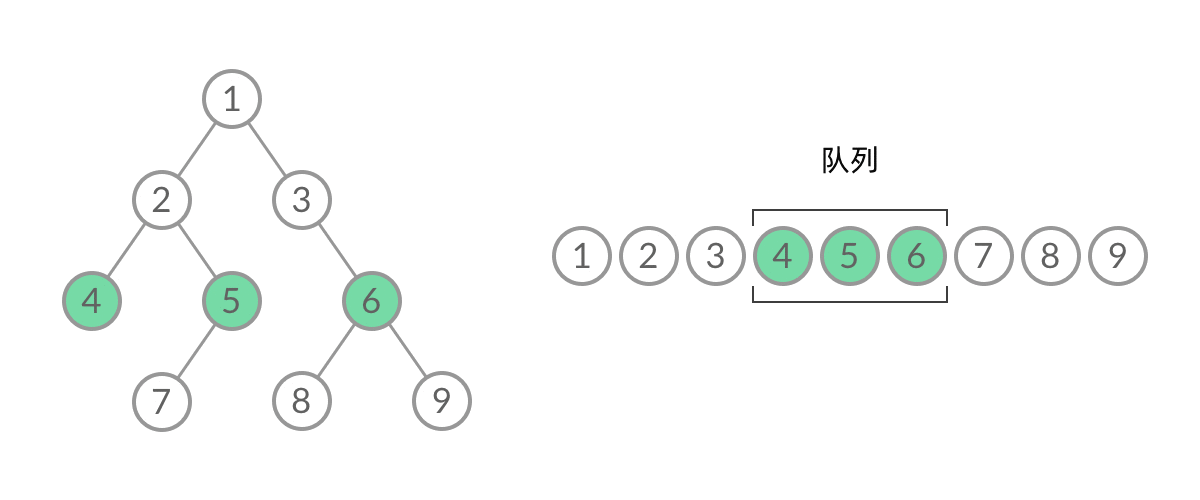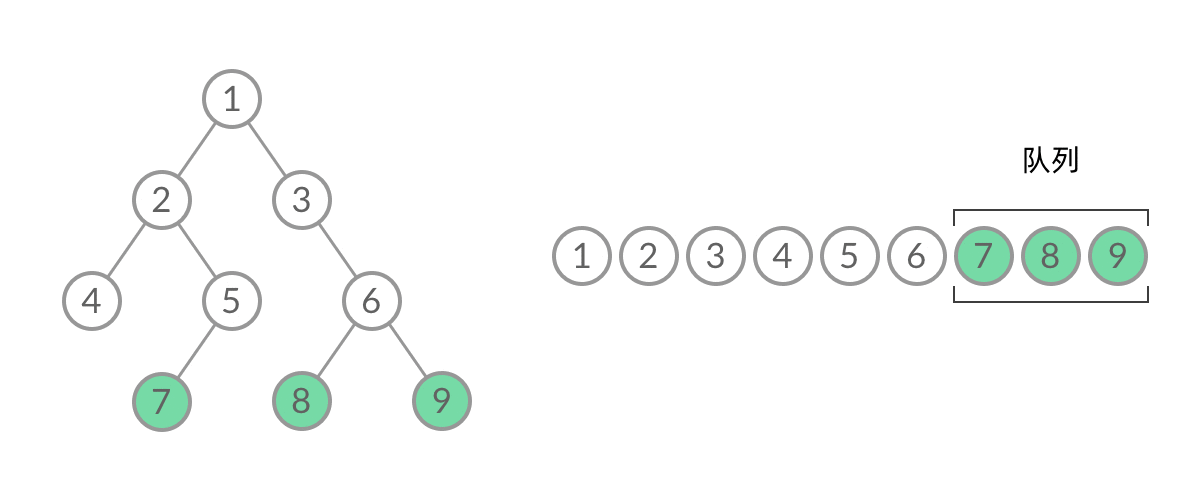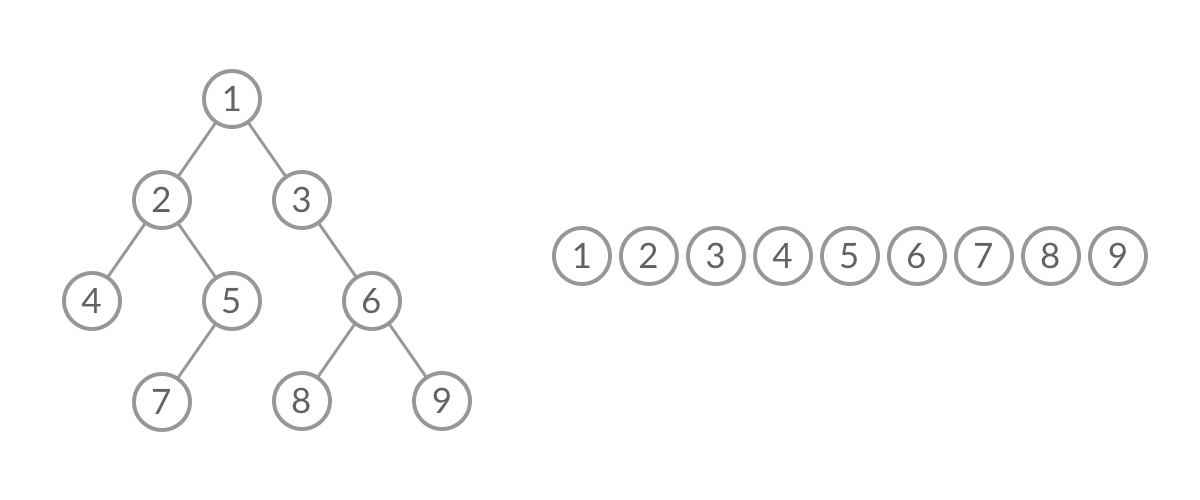
截取BFS遍历过程中的某个时刻：

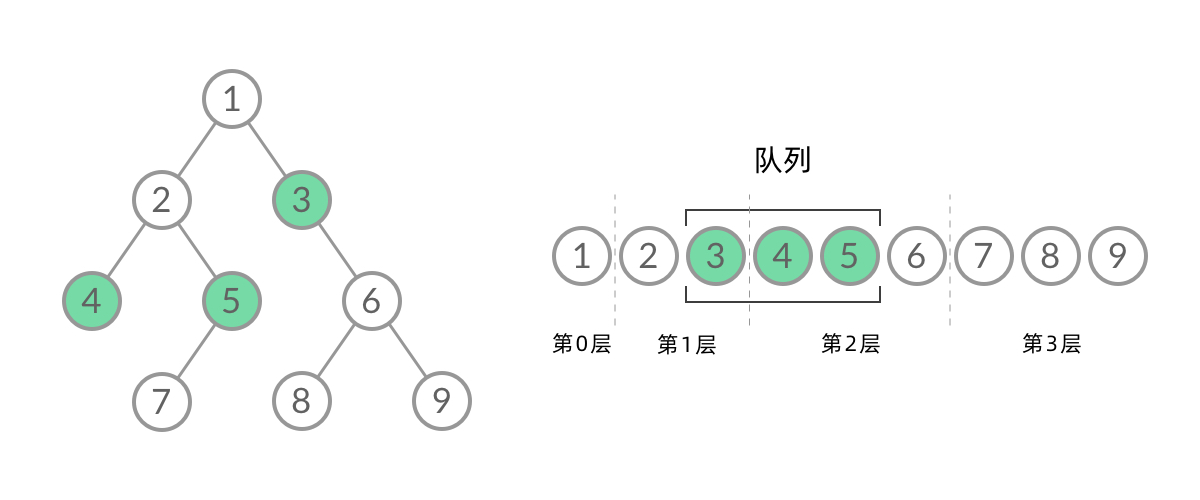
此时队列中的结点是 3、4、5，分别来自第 1 层和第 2 层。这个时候，第 1 层的结点还没处理结束，第 2 层的结点就压入队列中，导致两层的结点在队列中紧挨在一起，无法区分队列中的结点来自哪一层。

因此，在每一层遍历开始前，先记录队列中的结点数量 $n$ (也就是这一层的结点数量)，然后处理这一层的 $n$ 个结点：将 $n$个节点的值放入结果集中，将 $n$个节点的孩子放入队列中。

算法

广度优先搜索简直和这道题完美适配~

• 首先根元素入队
• 当队列不为空时
  • 求当前队列的长度$s_i$
  • 依次从队列中取$s_i$个元素进行拓展，结束后进入下一次迭代

这样做正确的理由：参考官方题解

它和 BFS 的区别在于 BFS 每次只取一个元素拓展，而这里每次取 $s_i$ 个元素。在上述过程中的第 $i$ 次迭代就得到了二叉树的第 $i$ 层的 $s_i$ 个元素。

复杂度分析

记树上所有节点的个数为 $n$。

• 时间复杂度： $O(n)$。每个点进队出队各一次，故渐进时间复杂度为$O(n)$。
• 空间复杂度：$O(n)$。队列中元素的个数不超过 nn 个，故渐进空间复杂度为 $O(n)$。

代码

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        res = []
        cur_level = [root]
        while cur_level:
            tmp = []
            next_level = []
            for node in cur_level:
                tmp.append(node.val)
                if node.left:
                    next_level.append(node.left)
                if node.right:
                    next_level.append(node.right)
            res.append(tmp)
            cur_level = next_level
        return re

使用双端队列：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:return []
        ans = []
        q = deque()
        q.append(root)
        while len(q):
            size = len(q)
            res = []
            for _ in range(size):
                t = q.popleft()
                res.append(t.val)
                if t.left:q.append(t.left)
                if t.right:q.append(t.right)
            ans.append(res)
        return ans

方法二：深度优先搜索

用dfs做这道题。就是每层带一个level属性。参考bfs/dfs

复杂度分析

• 时间复杂度：$O(n)$
• 空间复杂度：$O(h)$，$h$ 是树的高度

今天小苏喝了三碗汤。都是算法题，汤浓度有点点低~ 明天要看论文，修改之前的文章啦~

参考资料

BFS 的使用场景总结：层序遍历、最短路径问题(强烈推荐)

官方题解

bfs/dfs